多項式根

多項式 的根是一個數 ，使得 。 代數基本定理指出，一個 多項式 ，其次數為 ，有 個根，其中一些可能是重根。例如，多項式

(1)

的根是 、1 和 2。因此，求多項式的根等價於將多項式 因式分解 為 1 次因式。

任何 多項式 都可以進行數值因式分解，儘管不同的 演算法 有不同的優點和缺點。

多項式方程的根可以在 Wolfram 語言 中使用以下命令精確找到：Roots[lhs==rhs, var]，或者使用以下命令進行數值求解：NRoots[lhs==rhs, var]。一般而言，多項式 的給定根表示為Root[#^n+a[n-1]#^(n-1)+...+a[0]&, k]，其中 , 2, ..., 是標識特定根的索引，而純函式多項式是 不可約的。請注意，在 Wolfram 語言 中，根的排序在以下每個命令中都不同：Roots, NRoots, 以及Table[Root[p, k], k, n]。

在 Wolfram 語言 中，涉及Root物件的代數表示式可以使用以下命令組合成新的Root物件：RootReduce.

在這項工作中，多項式 的第 個根在 Wolfram 語言 的Root物件的排序中表示為 ，其中 是一個啞變數。在這種排序中，實根排在復根之前，並且 複共軛 根對是相鄰的。例如，

			(2)
			(3)

和

			(4)
			(5)
			(6)

設多項式

(7)

的 根 表示為 、 、 ...、 。那麼 韋達定理 給出

			(8)
			(9)
			(10)

這些可以透過寫出

(11)

展開，然後將係數與 (◇) 進行比較來推匯出來。

給定一個 次多項式 ，可以透過找到 矩陣

(12)

的 特徵值 來找到 根，並取 。這種方法計算量可能很大，但對於查詢接近和多重根非常穩健。

如果 多項式

(13)

的 係數 被指定為 整數，那麼有理根的 分子 必須是 的因子，而 分母 必須是 的因子（符號可以是正負）。這被稱為 多項式餘數定理。

如果一個 多項式 沒有 負 根（可以透過 笛卡爾符號法則 確定），那麼 最大下界 為 0。否則，寫出 係數，設 ，並計算下一行。現在，如果任何 係數 為 0，則將它們設定為負的下一個更高階 係數 的符號，從第二高階 係數 開始。如果所有符號交替，則 是最大下界。如果不是，則從 中減去 1，並計算另一行。例如，考慮 多項式

(14)

執行上述 演算法 然後給出

0	2	2		1
	2	0		8
--	2			8
	2			7
	2		5		35

因此，最大下界是 。

如果一個 多項式 沒有 正 根（可以透過 笛卡爾符號法則 確定），那麼 最小上界 為 0。否則，寫出 多項式 的 係數，必要時包括零。設 。在下一行，寫出最高階 係數。從第二高階 係數 開始，將 乘以剛剛寫出的數字加到原始的第二個 係數，並將其寫在第二個 係數 下面。繼續到零階。如果所有 係數 都是 非負的，則最小上界是 。如果不是，則將 加一，然後再次重複該過程。例如，取 多項式

(15)

執行上述 演算法 給出

0	2			1
1	2	1
2	2	3
3	2	5	8	25	68

因此，最小上界 是 3。

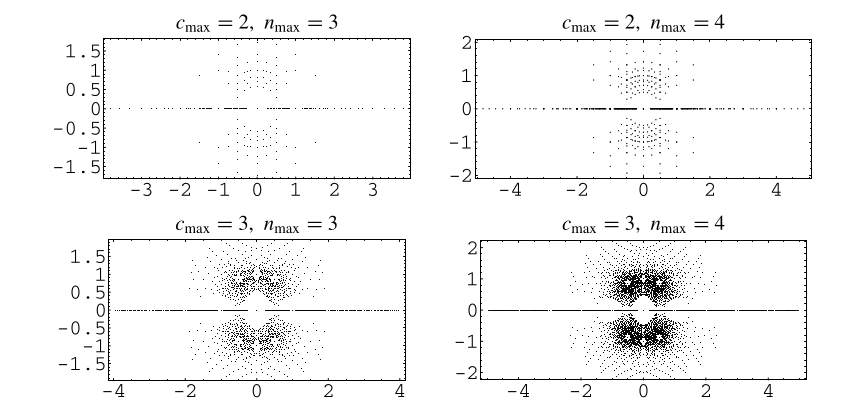
在複平面上繪製所有次數不超過某個次數且整數係數的絕對值小於某個截止整數的多項式的根，顯示了上面所示的美麗結構（Trott 2004，第 23 頁）。

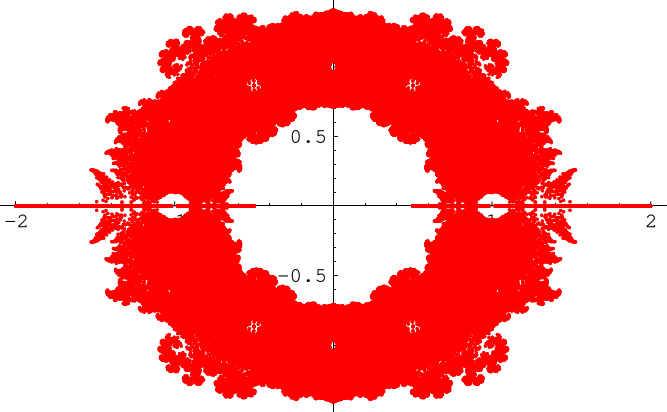
透過繪製所有係數為 且次數高達 的所有多項式的根，可以獲得更令人驚歎的圖形（Borwein 和 Jörgenson 2001；Pickover 2002；Bailey 等人 2007，第 18 頁）。