主題
Search

魏爾斯特拉斯 Zeta 函式

下載 Mathematica 筆記本下載 Wolfram 筆記本
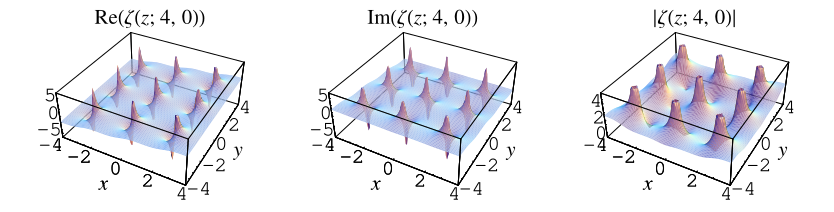
WeierstrassZetaReIm
WeierstrassZetaContours

魏爾斯特拉斯 zeta 函式 zeta(z;g_2,g_3) 是由下式定義的擬週期函式

(dzeta(z;g_2,g_3))/(dz)=-P(z;g_2,g_3),
(1)

其中 P(z;g_2,g_3) 是具有不變數 g_2 和 g_3 的 魏爾斯特拉斯橢圓函式，其中

lim_(z->0)[zeta(z;g_2,g_3)-z^(-1)]=0.
(2)

與其他 魏爾斯特拉斯橢圓函式 的情況一樣，橢圓不變數 g_2 和 g_3 通常為了簡潔而被省略。該函式在 Wolfram 語言 中實現為WeierstrassZeta[u, {g2, g3}]。

使用上面的定義得出

zeta(z)-z^(-1)=-int_0^z[P(z)-z^(-2)]dz
(3)
=-sum^'_(m,n=-infty)^inftyint_0^z[(z-Omega_(mn))^(-2)-Omega_(mn)^(-2)]dz,
(4)

其中 Omega_(mn)=2momega_1+2nomega_2，所以

zeta(z)=z^(-1)+sum^'_(m,n=-infty)^infty[(z-Omega_(mn))^(-1)+Omega_(mn)^(-1)+zOmega_(mn)^(-2)]
(5)

所以 zeta(z) 是一個 奇函式。積分 P(z+2omega_1)=P(z) 得到

zeta(z+2omega_1)=zeta(z)+2eta_1.
(6)

令 z=-omega_1 得到

zeta(-omega_1)+2eta_1=-zeta(omega_1)+2eta_1,
(7)

所以

eta_1=zeta(omega_1).
(8)

類似地，

eta_2=zeta(omega_2).
(9)

根據 Whittaker 和 Watson (1990)，

eta_1omega_2-eta_2omega_1=1/2pii.
(10)

如果 x+y+z=0，則

[zeta(x)+zeta(y)+zeta(z)]^2+zeta^'(x)+zeta^'(y)+zeta^'(z)=0
(11)

（Whittaker 和 Watson 1990，第 446 頁）。此外，

2(|1 P(x) P^2(x); 1 P(y) P^2(y); 1 P(z) P^2(z)|)/(|1 P(x) P^'(x); 1 P(y) P^'(y); 1 P(z) P^'(z)|)=zeta(x+y+z)-zeta(x)-zeta(y)-zeta(z)
(12)

（Whittaker 和 Watson 1990，第 446 頁）。

zeta(z) 的級數展開式由下式給出

zeta(z)=z^(-1)-sum_(k=2)^infty(c_kz^(2k-1))/(2k-1),
(13)

其中

c_2=(g_2)/(20)
(14)
c_3=(g_3)/(28)
(15)

和

c_k=3/((2k+1)(k-3))sum_(m=2)^(k-2)c_mc_(k-m)
(16)

對於 k>=4 （Abramowitz 和 Stegun 1972，第 635 頁）。因此，前幾個係數是

c_4=1/3c_2^2
(17)
c_5=3/(11)c_2c_3
(18)
c_6=1/(39)(2c_2^3+3c_3^2)
(19)
c_7=2/(33)c_2^2c_3
(20)
c_8=5/(7293)(11c_2^4+36c_3^2c_2).
(21)

另請參閱

魏爾斯特拉斯橢圓函式， 魏爾斯特拉斯 Sigma 函式

相關 Wolfram 網站

http://functions.wolfram.com/EllipticFunctions/WeierstrassZeta/, http://functions.wolfram.com/EllipticFunctions/WeierstrassZetaHalfPeriodValues/

使用 探索

參考文獻

Abramowitz, M. 和 Stegun, I. A. (編). "魏爾斯特拉斯橢圓函式和相關函式." 第 18 章，載於數學函式手冊，包含公式、圖表和數學表格，第 9 版。 紐約：Dover，第 627-671 頁，1972 年。Brezhnev, Y. V. "均勻化：關於 Burnside 曲線 y^2=x^5-x." 2001 年 12 月 9 日。 http://arxiv.org/abs/math.CA/0111150。Tölke, F. "特殊的魏爾斯特拉斯 Zeta 函式。" 第 8 章，載於實用函式論，第三卷：雅可比橢圓函式，勒讓德橢圓正規積分和特殊的魏爾斯特拉斯 Zeta 和 Sigma 函式。 柏林：Springer-Verlag，第 145-163 頁，1967 年。Whittaker, E. T. 和 Watson, G. N. "擬週期函式。函式 zeta(z)" 和 "函式 zeta(z) 的擬週期性。" 《現代分析教程，第 4 版。》第 20.4 和 20.41 節，英國劍橋：劍橋大學出版社，第 445-447 和 449-451 頁，1990 年。

在 上引用

魏爾斯特拉斯 Zeta 函式

請引用為

Weisstein, Eric W. "魏爾斯特拉斯 Zeta 函式。" 來自 --一個 Wolfram 網路資源。 https://mathworld.tw/WeierstrassZetaFunction.html

學科分類