主題
Search

槽弓形

DOWNLOAD Mathematica Notebook下載 Wolfram 筆記本
Arbelos

術語“槽弓形”在希臘語中意為鞋匠的刀，這個術語被應用於上圖中陰影區域，它類似於古代鞋匠使用的刀的刀片（Gardner 1979）。阿基米德本人被認為是第一個研究這個圖形的數學性質的數學家。中心凹口的位置是任意的，可以位於直徑上的任何位置。

槽弓形滿足許多意想不到的恆等式（Gardner 1979，Schoch）。

1. 將左右半圓的直徑分別稱為 r<1 和 1-r，因此外圍半圓的直徑為 1。那麼沿著槽弓形底部的弧長為

L=1/2[pir+pi(1-r)]=1/2pi,
(1)

因此，沿著外圍半圓的弧長與沿著兩個較小半圓的弧長相同。

2. 從兩個半圓的切線到大圓的邊緣繪製垂線 BD。那麼槽弓形的面積與直徑為 BD 的圓的面積相同。設 AC=1 且 r=AB，然後同時求解方程

r^2+h^2=x^2
(2)
(1-r)^2+h^2=y^2
(3)
x^2+y^2=1^2
(4)

對於邊

x=AD=sqrt(r)
(5)
y=CD=sqrt(1-r)
(6)
h=BD=sqrt(r(1-r)).
(7)
ArbelosRightTriangles

3. 在槽弓形上 BD 的每一半上內切的圓 C_1 和 C_1^' （稱為阿基米德圓）各自具有直徑 r(1-r)，或半徑 r(1-r)/2。

ArbelosAnnotated
ArbelosTriangles

可以使用上面顯示的三角形找到圓的位置。水平邊和斜邊的長度是已知的，如所示，因此可以使用勾股定理找到垂直邊。然後這給出了圓心為

x_1=r-R=1/2r(1+r)
(8)
y_1=sqrt(2rR)=rsqrt(1-r)
(9)

和

x_1^'=r+R=1/2r(3-r)
(10)
y_1^'=sqrt(2R(1-r))=(1-r)sqrt(r).
(11)

4. 令 A^' 為以 A 為中心且半徑為 r=AB 的圓與外圍半圓的交點，令 C^' 為以 C 為中心且半徑為 1-r=BC 的圓與外圍半圓的交點。那麼透過 A^' 且與 BD 相切的最小圓 C_2 等於透過 C^' 且與 BD 相切的最小圓 C_2^' (Schoch)。此外，這些圓的半徑 R 與阿基米德圓的半徑相同。求解

(x-1/2)^2+y^2=(1/2)^2
(12)

x^2+y^2=r^2
(13)

得到 (x,y)=(r^2,rsqrt(1-r^2))，因此 C_2 的中心為

x_2=r^2+1/2r(1-r)=1/2r(r+1)
(14)
y_2=rsqrt(1-r^2).
(15)

類似地，求解

(x-1/2)^2+y^2=(1/2)^2
(16)
(x-1)^2+y^2=(1-r)^2
(17)

得到 (x,y)=(r(2-r),(1-r)sqrt(r(2-r)))，因此 C_2^' 的中心為

x_2^'=r(2-r)-1/2r(1-r)=1/2r(r-3)
(18)
y_2^'=(1-r)sqrt(r(2-r)).
(19)
ArbelosArcs

5. 弧 BA^'、 BC^' 和 AA^'DC^'C 的圓的阿波羅尼斯圓 C_3 位於位置

x=1/2r(1+3r-2r^2)
(20)
y=r(1-r)sqrt((2-r)(1+r))
(21)

並且具有與阿基米德圓相同的半徑 R (Schoch)，透過 B 且與 C_3 相切的最小圓 C_3^' 也是如此。

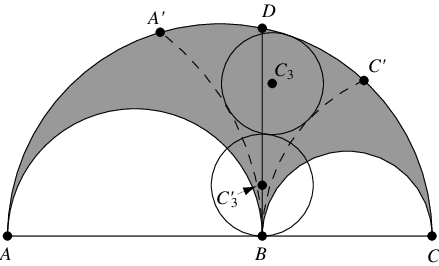
ArbelosApolloniusCircle

此外，令 B^'D^' 為透過圓 C_3 中心且平行於 BD 的直線，中心在 B^'D^' 上且與槽弓形的較小半圓相切的圓 C_3^('') 也具有半徑 R (Schoch)。 C_3^('') 的中心位置由下式給出

x_3^('')=x=1/2r(1+3r-2r^2)
(22)
y_3^('')=sqrt((1/2r+R)-(x-1/2r)^2)
(23)
=r(1-r)sqrt(1+r-r^2).
(24)
ArbelosApolloniusCircle3

D^' 的垂直 h^' 位置是

h^'=sqrt(1/4-1/4(2r^3-3r^2-r+1)^2)
(25)
=1/2sqrt(r(1-r)(2r^2-3r-1)(2r^2-r-2)).
(26)

6. 令 P 為 AB 的中點，令 Q 為 BC 的中點。然後繪製以 PQ 為直徑，中心為 M 的半圓。這個圓的半徑為

R_(PQ)=1/2{1-1/2[r+(1-r)]}=1/4.
(27)

透過 D^' 且與弧 PQ 相切的最小圓 C_4 也具有半徑 R (Schoch)。使用相似三角形，這個圓的中心位於

x_4=(r(2r^4-5r^3+3r+1))/(1+4r-4r^2)
(28)
y_4=(2r^2-2r-1)/(2(4r^2-4r-1))sqrt(r(1-r)(2r^2-3r-1)(2r^2-r-2)).
(29)

類似地，令 U 為 B^'D^' 和 半圓 PQ 的交點，那麼透過 B、 B^' 和 U 的圓也具有半徑 R (Schoch)。這個圓的中心位於

x_4^'=1/4r(3+3r-2r^2)
(30)
y_4^'=1/4r(1-r)sqrt((2r+1)(3-2r)).
(31)
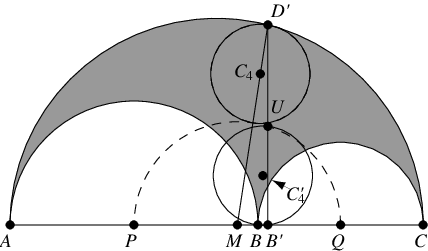
ArbelosC4-12

考慮半徑為 r_X 的圓 X，它與兩個內部半圓相切。其位置和半徑透過求解以下聯立方程獲得

h^2+z^2=(1/2r+r_X)^2
(32)
h^2+(1/2-z)^2=[1/2(1-r)+r_X]^2
(33)
(1/2r+r_X)^2+[1/2(1-r)+r_X]^2=(1/4)^2,
(34)

給出

z=1/4+1/4(2r-1)sqrt(1+4r-4r^2)
(35)
h=r(1-r)
(36)
r_X=1/4(sqrt(1+4r-4r^2)-1).
(37)

令 C_4^('') 為透過 X 且與 ABC 相切的最小圓，因此 C_4^('') 的半徑為 h/2=r(1-r)/2=R (Schoch)，其中心位於

x_4^('')=1/4+1/2r+1/4(2r-1)sqrt(1+4r-4r^2)
(38)
y_4^('')=1/2r(1-r).
(39)
ArbelosC4-3

7. 在槽弓形的每個小半圓內，構造類似於原始槽弓形的槽弓形。那麼圓 C_5 和 C_5^' 是全等的，並且具有半徑 R (Schoch)。此外，連線弧的中點及其尖點以形成矩形 EFGH 和 E^'F^'G^'H^'。那麼這些矩形相對於點 C_5^('') 是相似的 (Schoch)。這個點位於直線 B^'D^' 上，並且以 C_5^('') 為中心且半徑為 C_5^('')B^' 的圓也具有半徑 R，因此 C_5^('') 的座標為 (1/2r(1+3r-2r^2),1/2r(1-r))。下表總結了矩形頂點的位置。

X座標X^'座標
E(1/2r,1/2r)E^'(r(2-r),0)
F(1/2r(1+r),1/2r(1-r))F^'(1/2r(3-r),1/2r(1-r))
G(r^2,0)G^'(1/2(1+r),1/2(1-r))
H(1/2r^2,1/2r^2)H^'(1/2(1+2r-r^2),1/2(1-r)^2)
ArbelosC5

8. 令 MM^' 為 AC 的垂直平分線，令 B 為槽弓形的尖點，D 位於其上方，令 E 和 G^' 分別為大半圓和小半圓的頂部。令 EG^' 與直線 MM^' 和 BD 相交於點 I 和 J。那麼透過 I 且與弧 AC 在 M^' 處相切的最小圓 C_6，透過 J 且與外側半圓在 P_C 處相切的最小圓 C_6^'，以及以 JB 為直徑的圓 C_6^('') 都是阿基米德圓 (Schoch)。圓 C_6^('') 稱為班剋夫圓，並且也是點 B 和第一個帕普斯圓鏈的切點 P_A 和 P_C 的外接圓。圓 C_6、 C_6^' 和 C_6^('') 的中心由下式給出

x_6=1/2
(40)
y_6=1/2(1-r+r^2)
(41)
x_6^'=(r(1-r+2r^2))/(2(1-2r+2r^2))
(42)
y_6^'=(r(1-r)(1-r+r^2))/(1-2r+2r^2)
(43)
x_6^('')=r
(44)
y_6^('')=1/2r(1-r).
(45)

非常令人驚訝的是，點 E、 M、 B、 G^'、 P_C、 D 和 M^' 是共圓的 (Schoch)，位於中心為 ((1+2r)/4,1/4) 且半徑為

R_(EMBG^'P_CDM^')=1/4sqrt(2(1-2r+2r^2)).
(46)
ArbelosC6

9. 阿基米德圓的最小外接圓的面積等於槽弓形的面積。

ArbelosCircumcircle

10. 與半圓 AB 和 BC 相切的直線包含點 E 和 F，它們分別位於直線 AD 和 CD 上。此外，BD 和 EF 互相平分，並且點 B、 D、 E 和 F 是共圓的。

ArbelosAnnotated2

11. 構造一個相切圓鏈，從與兩個小圓和一個大圓相切的圓開始。這個鏈被稱為帕普斯鏈，其圓的中心位於一個橢圓上，該橢圓的焦點位於界定它的半圓的中心。此外，第 n 個圓 C_n 的直徑是到半圓底邊的垂直距離的 (1/n) 分之一。這個結果最容易使用反演來證明，但帕普斯就知道這個結果，他稱之為古代定理（Hood 1961，Cadwell 1966，Gardner 1979，Bankoff 1981）。

12. 公切線 EF （見 10）和大半圓和第一個帕普斯圓的公切線在直線 AB 上相交。

PappusChain

13. 如果 B 以黃金比例 phi 分割 AC，那麼鏈中的圓滿足許多其他特殊性質 (Bankoff 1955)。

參見

阿基米德圓, 阿基米德圓, 班剋夫圓, 考克斯特的正切圓的對數螺線序列, 黃金比例, 反演, 帕普斯鏈, 肖赫線, 施泰納鏈, 相切圓, 戰斧, 吳圓

使用 探索

參考文獻

Allanson, B. "Pappus's Arbelos" Java applet. http://members.ozemail.com.au/~llan/arbelos.html.Bankoff, L. "The Fibonacci Arbelos." Scripta Math. 20, 218, 1954.Bankoff, L. "The Golden Arbelos." Scripta Math. 21, 70-76, 1955.Bankoff, L. "Are the Twin Circles of Archimedes Really Twins?" Math. Mag. 47, 214-218, 1974.Bankoff, L. "How Did Pappus Do It?" In The Mathematical Gardner (Ed. D. Klarner). Boston, MA: Prindle, Weber, and Schmidt, pp. 112-118, 1981.Bankoff, L. "The Marvelous Arbelos." In The Lighter Side of Mathematics (Ed. R. K. Guy and R. E. Woodrow). Washington, DC: Math. Assoc. Amer., 1994.Boas, H. P. "Reflections on the Arbelos." Preprint based on the Nineteenth Annual Rose-Hulman Undergraduate Mathematics Conference, March 15, 2002. Oct. 26, 2004. http://www.math.tamu.edu/~harold.boas/preprints/arbelos.pdf.Bogomolny, A. "Arbelos--The Shoemaker's Knife." http://www.cut-the-knot.org/proofs/arbelos.shtml.Cadwell, J. H. Topics in Recreational Mathematics. Cambridge, England: Cambridge University Press, 1966.Coolidge, J. L. A Treatise on the Geometry of the Circle and Sphere. New York: Chelsea, pp. 35-36, 1971.Dodge, C. W. Euclidean Geometry and Transformations. New York: Dover, 2004.Dodge, C. W.; Schoch, T.; Woo, P. Y.; and Yiu, P. "Those Ubiquitous Archimedean Circles." Math. Mag. 72, 202-213, 1999.Gaba, M. G. "On a Generalization of the Arbelos." Amer. Math. Monthly 47, 19-24, 1940.Gardner, M. "Mathematical Games: The Diverse Pleasures of Circles that Are Tangent to One Another." Sci. Amer. 240, 18-28, Jan. 1979.Heath, T. L. The Works of Archimedes with the Method of Archimedes. New York: Dover, p. 307, 1953.Hood, R. T. "A Chain of Circles." Math. Teacher 54, 134-137, 1961.Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA: Houghton Mifflin, pp. 116-117, 1929.Ogilvy, C. S. Excursions in Geometry. New York: Dover, pp. 54-55, 1990.Okumura, H. and Watanabe, M. "The Archimedean Circles of Schoch and Woo." Forum Geom. 4, 27-34, 2004. http://forumgeom.fau.edu/FG2004volume4/FG200404index.html.Okumura, H. and Watanabe, M. "The Twin Circles of Archimedes in a Skewed Arbelos." Forum Geom. 4, 229-251, 2004. http://forumgeom.fau.edu/FG2004volume4/FG200428index.html.Okumura, H. and Watanabe, M. "The Arbelos in n-Aliquot Parts." Forum Geom. 5, 37-45, 2005. http://forumgeom.fau.edu/FG2005volume5/FG200506index.html.Power, F. "Some More Archimedean Circles in the Arbelos." Forum Geom. 5, 133-134, 2005. http://forumgeom.fau.edu/FG2005volume5/FG200517index.html.Schoch, T. "Arbelos: Amazing Properties." http://www.retas.de/thomas/arbelos/arbelos.html.Schoch, T. "A Dozen More Arbelos Twins." http://www.retas.de/thomas/arbelos/biola/.Soddy, F. "The Bowl of Integers and the Hexlet." Nature 139, 77-79, 1937.Wells, D. The Penguin Dictionary of Curious and Interesting Geometry. London: Penguin, pp. 5-6, 1991.Update a linkWoo, P. "The Arbelos." http://www-students.biola.edu/~woopy/math/arbelos.htmWoo, P. Y. "Simple Construction for the Incircle of an Arbelos." Forum Geom. 1, 133-136, 2001. http://forumgeom.fau.edu/FG2001volume1/FG200119index.html.Yiu, P. "The Archimedean Circles in the Shoemaker's Knife." Lecture at the 31st Annual Meeting of the Florida Section of the Math. Assoc. Amer., Boca Raton, FL, March 6-7, 1998.

請引用為

Weisstein, Eric W. "槽弓形." 來自 Web 資源。 https://mathworld.tw/Arbelos.html

主題分類