七邊形三角形

由正 七邊形 的三個頂點形成的唯一（模旋轉）不等邊三角形，其頂角為 、 和 。 有許多神奇的公式將七邊形三角形的邊和角聯絡起來（Bankoff 和 Garfunkel 1973）。

三角形的 面積 為

其中 是三角形的 外接圓半徑。 七邊形三角形的邊長的平方和等於 （Bankoff 和 Garfunkel 1973）。 內切圓半徑 與 外接圓半徑 的比率 由以下方程的正根給出

邊長滿足

（Bankoff 和 Garfunkel 1973）和

後者可以透過將 托勒密定理 應用於邊長為 、 、 和 ，對角線為 和 的四邊形，然後除以 來輕鬆證明（I. Larrosa Cañestro，私人通訊，2006 年 4 月 23 日）。

布羅卡角 滿足

並且 旁切圓半徑 等於 的 九點圓 的半徑。

是另外兩條邊的 調和平均數 的一半，

對於變數的所有排列組合等式都成立（Bankoff 和 Garfunkel 1973）。 此外，

如果 、 和 是高，則

如果 、 和 是高的垂足，則

等等（Bankoff 和 Garfunkel 1973）。 角 和 的內角平分線等於鄰邊之差，角 的外角平分線等於鄰邊之和。

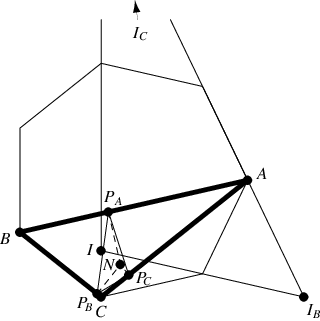
連線七邊形三角形的角平分線的垂足的三角形 是 等腰三角形，其中 。

垂心三角形 和 中線三角形 是全等且透視的。 此外，兩者都類似於 、 關於 九點中心 的 垂足三角形 以及由 內心 和外角平分線 和 形成的三角形 （Bankoff 和 Garfunkel 1973）。 三角形 也類似於這些三角形。

還有大量有趣的三角恆等式與七邊形三角形的角度有關

（Bankoff 和 Garfunkel 1973）。

此外，

最後，七邊形三角形滿足以下其他性質

1. 第一個 布羅卡點 對應於 九點中心，第二個 布羅卡點 位於 九點圓 上。

2. ，其中 是 外心， 是 垂心， 是 外接圓半徑。

3. ，其中 是 內心， 是 內切圓半徑。

4. 從 垂心 到七邊形三角形的 外接圓 的兩條切線互相垂直。

5. 切線三角形 的 外接圓 的中心與 關於 的對稱點重合。

6. 從 出發的高是角 的內角平分線長度的一半。