最大公約數

最大公約數，有時也稱為最高公約數 (Hardy and Wright 1979, p. 20)，是兩個正整數 和 最大的共同約數，即 和 都能被它整除。例如，，，和 。最大公約數 也可以定義為三個或更多正整數的最大公約數，即它們共有的最大約數。最大公約數為 1 的兩個或多個正整數被稱為彼此互質，通常簡稱為“互質”。

各種符號約定總結在下表中。

符號	來源
	本作品，Zwillinger (1996, p. 91), Råde and Westergren (2004, p. 54)
	Gellert et al. (1989, p. 25), D'Angelo and West (1990, p. 13), Graham et al. (1990, p. 103), Bressoud and Wagon (2000, p. 7), Yan (2002, p. 30), Bronshtein et al. (2007, pp. 323-324), Wolfram Language
g.c.d.	Andrews 1994, p. 22

, , ... 的最大公約數在 Wolfram Language 中實現為GCD[a, b, ...].

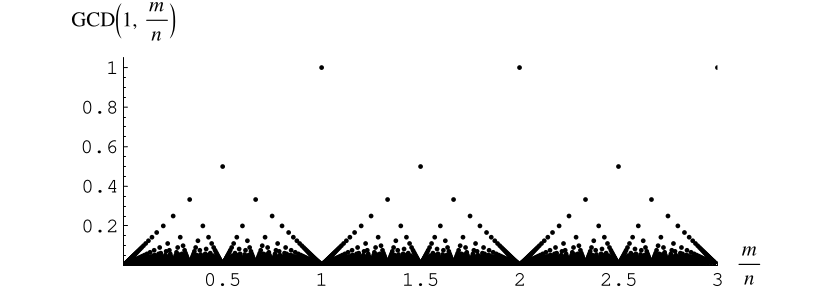
上圖顯示了 與有理數 的關係。這裡， 是最大的有理數 ，對於它，所有的 都是整數。很容易看出，如果 ，其中 ，那麼 。此外，如果透過將 擴充套件為當 是無理數時，其值等於 0，則得到的函式在無理數處連續，在有理數處不連續，並且在任何有限區間上的黎曼積分等於 0。

以上圖表顯示了 在 -平面中的一些視覺化表示。左圖是簡單的 ，中間的圖是 的二維離散傅立葉變換的絕對值 (Trott 2004, pp. 25-26)，右圖是 變換的絕對值。

如果 是 和 的最大公約數，那麼 是滿足以下條件的最大可能整數

			(1)
			(2)

其中 和 是正整數。

歐幾里得演算法可以用來求兩個整數的最大公約數，並找到整數 和 使得

(3)

這個概念也可以推廣到比整數 更一般的環。然而，即使對於歐幾里得環，兩個環元素的 GCD 的概念與環的兩個理想的 GCD 概念也不同。當研究除 以外的環（例如多個變數的多項式環）時，這有時會成為混淆的來源。

為了計算 GCD，寫出 和 的素因數分解，

			(4)
			(5)

其中 s 是 和 的所有素因子，並且如果 沒有在一個因式分解中出現，則相應的指數取為 0。那麼最大公約數 由下式給出

(6)

其中 min 表示最小值。例如，考慮 。

			(7)
			(8)

所以

(9)

GCD 是可分配的

(10)

(11)

且是結合性的

			(12)
			(13)
			(14)

如果 且 ，則

			(15)
			(16)

所以 。GCD 也是冪等的

(17)

交換律

(18)

並滿足吸收律

(19)

對於正奇數 和 ，收斂到 的遞迴方程由下式給出

(20)

其中 和 ，其中 是 在 中的最大整除指數 (Stehlé and Zimmerman 2004)。上圖顯示了奇數 收斂所需的迭代次數。

隨機選擇的兩個整數互質的機率為 ，其中 是黎曼 zeta 函式。Polezzi (1997) 觀察到 ，其中 是平面上連線向量 (0, 0) 和 的直線上的格點數（不包括 本身）。這個觀察結果與獲得互質整數的機率密切相關，也與既約分數 的幾何解釋有關，即作為穿過格點的字串，端點為 (1,0) 和 。它壓在 上的釘子給出了 的交替收斂項，是 的連分數，而其他收斂項是從它壓在釘子上獲得的，初始端點為 (0, 1)。

Knuth 證明了

(21)