主題
Search

隨機矩陣

DOWNLOAD Mathematica Notebook下載 Wolfram 筆記本

隨機矩陣是給定型別和大小的矩陣，其條目由來自指定分佈的隨機陣列成。

隨機矩陣理論被引為凱瑟琳在 2005 年電影證明中證明素數定理中一個重要結果時使用的“現代工具”之一。

對於具有實n×n矩陣，其元素具有標準正態分佈，實特徵值的期望數量由下式給出

E_n=1/2+sqrt(2)(_2F_1(1,-1/2;n;1/2))/(B(n,1/2))
(1)
={sqrt(2)sum_(k=0)^(n/2-1)((4k-1)!!)/((4k)!!) for n even; 1+sqrt(2)sum_(k=1)^((n-1)/2)((4k-3)!!)/((4k-2)!!) for n odd,
(2)

其中 _2F_1(a,b;c;z) 是超幾何函式，B(z,a) 是beta 函式（Edelman等， 1994；Edelman 和 Kostlan 1994）。E_n 具有漸近行為

E_n∼sqrt((2n)/pi).
(3)

令 p_(n,k) 為在n×n矩陣的復譜中恰好有 k 個實特徵值的機率。Edelman (1997) 表明

p_(n,n)=2^(-n(n-1)/4),
(4)

這是所有 p_(n,k)s 中最小的機率。Kanzieper 和 Akemann (2005) 推匯出了高斯實隨機矩陣譜中預期實特徵值數量的整個機率函式，如下所示

p_(n,k)=p_(n,n)F_l(p_1,...,p_l),
(5)

其中

F_l(p_1,...,p_l)=(-1)^lsum_(|lambda|=l)product_(j=1)^(g)1/(sigma_j!)(-(p_(l_j))/(l_j))^(sigma_j)
(6)
=1/(l!)Z_((1^l))(p_1,...,p_l).
(7)

在 (6) 中，求和執行在所有長度為 l 的劃分 lambda 上，l 是複共軛特徵值對的數量，Z_((1^l)) 是區域多項式。此外，(6) 使用了劃分 lambda 的頻率表示（Kanzieper 和 Akemann 2005）。引數 p_l 取決於 n（矩陣維度）的奇偶性，並由下式給出

p_j=Tr_((0,|_n/2_|-1))rho^^^j,
(8)

其中 Tr(A) 是矩陣跡，rho^^ 是一個 m×m 矩陣，其條目為

rho^^_(alpha,beta)^(even)=int_0^inftyy^(2(beta-alpha)-1)e^(y^2)erfc(ysqrt(2))×[(2alpha+1)L_(2alpha+1)^(2(beta-alpha)-1)(-2y^2)+2y^2L_(2alpha-1)^(2(beta-alpha)+1)(-2y^2)]dy
(9)
rho^^_(alpha,beta)^(odd)=rho^^_(alpha,beta)^(even)-(-4)^(m-beta)(m!)/((2m)!)((2beta)!)/(beta!)rho^^_(alpha,beta)^(even),
(10)

alpha 和 beta 在 0 和 m-1 之間變化，m=|_n/2_|，其中 |_x_| 是向下取整函式），L_j^alpha(z) 是廣義拉蓋爾多項式，erfc(z) 是互補誤差函式 erfc (Kanzieper 和 Akemann 2005)。

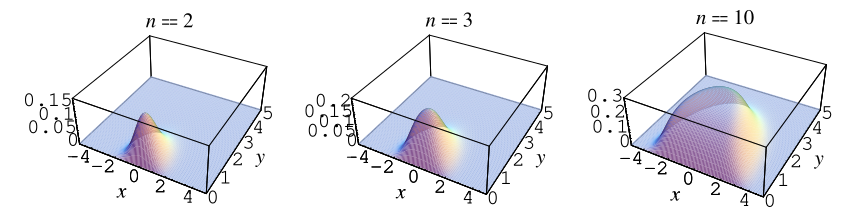
RandomMatrixComplexEigenvalues

Edelman (1997) 證明了實n×n矩陣的隨機複共軛特徵值對 x+/-iy 的密度，該矩陣的元素取自標準正態分佈，為

rho_n(x,y)=sqrt(2/pi)ye^(y^2-x^2)erfc(sqrt(2)y)e_(n-2)(x^2+y^2)
(11)
=sqrt(2/pi)e^(2y^2)yerfc(sqrt(2)y)(Gamma(n-1,x^2+y^2))/(Gamma(n-1))
(12)

對於 y>=0，其中 erfc(z) 是 erfc（互補誤差）函式，e_n(z) 是指數和函式，Gamma(a,x) 是上不完全伽馬函式。在上半平面上積分（並乘以 2）得到復特徵值的期望數量為

c_n=2int_(-infty)^inftyint_0^inftyrho_n(x,y)dydx
(13)
=n-1/2-sqrt(2)(_2F_1(1,-1/2;n;1/2))/(B(n,1/2))
(14)
=n-1/2-(2n-1)!!2^(-n)_2F^~_1(n-1,-1/2;n;-1)
(15)

（Edelman 1997）。前幾個值為

c_1=0
(16)
c_2=2-sqrt(2)
(17)
c_3=2-1/2sqrt(2)
(18)
c_4=4-(11)/8sqrt(2)
(19)
c_5=4-(13)/(16)sqrt(2)
(20)

（OEIS A052928，A093605 和 A046161）。

吉爾科圓律考慮了一組隨機n×n 實矩陣的特徵值 lambda（可能是複數），這些矩陣的條目是獨立的並取自標準正態分佈，並指出當 n->infty 時，lambda/sqrt(n) 在複平面中的單位圓盤上均勻分佈。

維格納半圓律指出，對於大的 n×n 對稱實矩陣，其元素取自分佈，滿足某些相當一般的性質，特徵值的分佈是半圓函式。

如果從以下矩陣中以 1/2 的機率選擇 n 個矩陣 M_i 之一

M_+=[0 1; 1 1]
(21)
M_-=[0 1; 1 -1],
(22)

那麼

lim_(n->infty)(ln||M_1...M_n||)/n=c,
(23)

其中 e^c=1.13198824... （OEIS A078416）和 ||M|| 表示矩陣譜範數（Bougerol 和 Lacroix 1985，第 11 頁和 157 頁；Viswanath 2000）。這與隨機斐波那契數列中出現的常數相同。以下 Wolfram 語言 程式碼可用於估計此常數。

  With[{n = 100000},
    m = Fold[Dot, IdentityMatrix[2],
      {{0, 1}, {1, #}}& /@
        RandomChoice[{-1, 1}, {n}]
    ] // N;
    Log[Sqrt[Max[Eigenvalues[Transpose[m] . m]]]] /
    n
  ]

另請參閱

復矩陣，吉爾科圓律，整數矩陣，矩陣，隨機斐波那契數列，實矩陣，維格納半圓律

使用 探索

參考文獻

Bougerol, P. 和 Lacroix, J. 隨機矩陣乘積及其在薛定諤運算元中的應用。 巴塞爾，瑞士：Birkhäuser，1985 年。Chassaing, P.; Letac, G.; 和 Mora, M. “Brocot 序列和 SL_2(R) 上的隨機遊走。” 在群 VII 上的機率測度（H. Heyer 編輯）。紐約：Springer-Verlag，1984 年，第 36-48 頁。Edelman, A. “隨機實高斯矩陣具有 k 個實特徵值的機率，相關分佈和圓律。” J. Multivariate Anal. 60, 203-232, 1997.Edelman, A. 和 Kostlan, E. “隨機多項式有多少個實零點？” Bull. Amer. Math. Soc. 32, 1-37, 1995.Edelman, A.; Kostlan, E.; 和 Shub, M. “隨機矩陣有多少個實特徵值？” J. Amer. Math. Soc. 7, 247-267, 1994.Furstenberg, H. “非交換隨機乘積。” Trans. Amer. Math. Soc. 108, 377-428, 1963.Furstenberg, H. 和 Kesten, H. “隨機矩陣的乘積。” Ann. Math. Stat. 31, 457-469, 1960.Girko, V. L. 隨機行列式理論。 波士頓，MA：Kluwer，1990 年。Kanzieper, E. 和 Akemann, G. “Ginibre 隨機實矩陣系綜中實特徵值的統計。” Phys. Rev. Lett. 95, 230201-1-230201-4, 2005.Katz, M. 和 Sarnak, P. 隨機矩陣、弗羅貝尼烏斯特徵值和單值性。 普羅維登斯，羅德島州：Amer. Math. Soc., 1999.Lehmann, N. 和 Sommers, H.-J. “隨機實矩陣的特徵值統計。” Phys. Rev. Let. 67, 941-944, 1991.Mehta, M. L. 隨機矩陣，第 3 版。 紐約：Academic Press，1991 年。Sloane, N. J. A. “整數序列線上百科全書”中的序列 A046161，A052928，A078416 和 A093605。Viswanath, D. “隨機斐波那契數列和數字 1.13198824....” Math. Comput. 69, 1131-1155, 2000.

在 上引用

隨機矩陣

請引用為

Weisstein, Eric W. “隨機矩陣”。來自 Web 資源。 https://mathworld.tw/RandomMatrix.html

主題分類