beta 函式  是勒讓德和惠特克與沃森 (1990) 對 beta 積分(也稱為第一類尤拉積分)使用的名稱。它由下式定義:
是勒讓德和惠特克與沃森 (1990) 對 beta 積分(也稱為第一類尤拉積分)使用的名稱。它由下式定義:
 |
(1)
|
beta 函式  在 Wolfram 語言 中實現為Beta[a, b]。
在 Wolfram 語言 中實現為Beta[a, b]。
為了推導 beta 函式的積分表示,將兩個階乘的乘積寫成:
 |
(2)
|
現在,令  ,
, ,則
,則
使用  ,
, 變換到 極座標:
變換到 極座標:
然後 beta 函式定義為:
重寫自變數,得到 beta 函式的常用形式:
根據對稱性,
 |
(13)
|
一般三角形式為:
 |
(14)
|
透過令  ,方程 (14) 可以轉換為關於多項式的積分:
,方程 (14) 可以轉換為關於多項式的積分:
對於任何  且
且 ![R[z_1],R[z_2]>0](/images/equations/BetaFunction/Inline51.svg) ,
,
 |
(19)
|
(Krantz 1999,第 158 頁)。
為了將其轉換為可用於推導 勒讓德倍增公式 的形式,令  ,則
,則  且
且  ,以及
,以及
為了將其轉換為可用於開發 貝塞爾函式 和 超幾何函式 的積分表示的形式,令  ,則
,則
 |
(22)
|
beta 函式的導數由下式給出:
其中  是多伽瑪函式。
是多伽瑪函式。
可以使用 高斯乘法公式 推匯出各種恆等式:
其他恆等式包括:
 |
(32)
|
 |
(33)
|
如果  是一個正整數,則
是一個正整數,則
 |
(34)
|
此外,
 |
(35)
|
 |
(36)
|
beta 函式也由以下乘積給出:
 |
(37)
|
(Andrews et al. 1999,第 8 頁)。
Gosper 給出了通用公式:
![product_(i=0)^(2n)B(i/(2n+1)+a,i/(2n+1)+b)
=((2n+1)^((2n+1)/2)pi^nB(n,1/2[(b+a)(2n+1)+1])B(a(2n+1),b(2n+1)))/((n-1)!)](/images/equations/BetaFunction/NumberedEquation13.svg) |
(38)
|
對於奇數  ,以及
,以及
 |
(39)
|
這是 gamma 函式 的類似恆等式的直接結果。將  和
和  代入上述公式,得到特殊情況:
代入上述公式,得到特殊情況:
 |
(40)
|
![B(a,b)B(a+1/4,b+1/4)B(a+1/2,b+1/2)B(a+3/4,b+3/4)
=(2^(3-4(a+b))pi^2B(4a,4b))/((a+b)[1+4(a+b)]B(2(a+b),2(a+b+1))).](/images/equations/BetaFunction/NumberedEquation16.svg) |
(41)
|
另請參閱
Beta 積分、
中心 Beta 函式、
狄利克雷 Beta 函式、
狄利克雷積分、
Gamma 函式、
不完全 Beta 函式、
正則化 Beta 函式
相關 Wolfram 網站
http://functions.wolfram.com/GammaBetaErf/Beta/
使用 探索
參考文獻
Abramowitz, M. and Stegun, I. A. (Eds.). "Beta Function" and "Incomplete Beta Function." §6.2 and 6.6 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 258 and 263, 1972.Andrews, G. E.; Askey, R.; and Roy, R. Special Functions. Cambridge, England: Cambridge University Press, 1999.Bailey, D. H.; Borwein, P. B.; and Plouffe, S. "On the Rapid Computation of Various Polylogarithmic Constants." Math. Comput. 66, 903-913, 1997.Arfken, G. "The Beta Function." §10.4 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 560-565, 1985.Erdélyi, A.; Magnus, W.; Oberhettinger, F.; and Tricomi, F. G. "The Beta Function." §1.5 in Higher Transcendental Functions, Vol. 1. New York: Krieger, pp. 9-13, 1981.Jeffreys, H. and Jeffreys, B. S. "The Beta Function." §15.02 in Methods of Mathematical Physics, 3rd ed. Cambridge, England: Cambridge University Press, pp. 463-464, 1988.Koepf, W. Hypergeometric Summation: An Algorithmic Approach to Summation and Special Function Identities. Braunschweig, Germany: Vieweg, pp. 6-9, 1998.Krantz, S. G. "The Beta Function." §13.1.11 in Handbook of Complex Variables. Boston, MA: Birkhäuser, pp. 157-158, 1999.Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, p. 425, 1953.Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Gamma Function, Beta Function, Factorials, Binomial Coefficients" and "Incomplete Beta Function, Student's Distribution, F-Distribution, Cumulative Binomial Distribution." §6.1 and 6.2 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 206-209 and 219-223, 1992.Spanier, J. and Oldham, K. B. "The Incomplete Beta Function  ." Ch. 58 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 573-580, 1987.Whittaker, E. T. and Watson, G. N. A Course of Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, 1990.
." Ch. 58 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 573-580, 1987.Whittaker, E. T. and Watson, G. N. A Course of Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, 1990.在 上引用
Beta 函式
請引用本文為
Weisstein, Eric W. "Beta 函式。" 來自 Web 資源。https://mathworld.tw/BetaFunction.html
主題分類
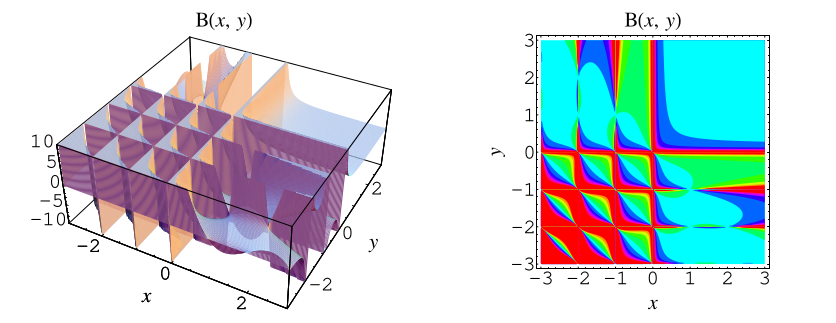
是勒讓德和惠特克與沃森 (1990) 對 beta 積分(也稱為第一類尤拉積分)使用的名稱。它由下式定義:
在 Wolfram 語言 中實現為Beta[a, b]。
,
,則
,
變換到 極座標:
且
,
,則
且
,以及
,則
是多伽瑪函式。

是一個正整數,則

![product_(i=0)^(2n)B(i/(2n+1)+a,i/(2n+1)+b)
=((2n+1)^((2n+1)/2)pi^nB(n,1/2[(b+a)(2n+1)+1])B(a(2n+1),b(2n+1)))/((n-1)!)](/images/equations/BetaFunction/NumberedEquation13.svg)
,以及

和
代入上述公式,得到特殊情況:
![B(a,b)B(a+1/4,b+1/4)B(a+1/2,b+1/2)B(a+3/4,b+3/4)
=(2^(3-4(a+b))pi^2B(4a,4b))/((a+b)[1+4(a+b)]B(2(a+b),2(a+b+1))).](/images/equations/BetaFunction/NumberedEquation16.svg)