莫比烏斯帶,也稱為扭曲柱面(Henle 1994,第 110 頁),是一種單側不可定向曲面,透過將一個閉合帶切成一個條狀,將由此產生的兩個端部之一扭轉半圈,然後重新連線兩個端部而獲得(右圖;Gray 1997,第 322-323 頁)。以他的名字命名的帶是由莫比烏斯在 1858 年發明的,儘管它是由 Listing 獨立發現的,Listing 發表了它,而莫比烏斯沒有發表(Derbyshire 2004,第 381 頁)。與柱面一樣,它不是真正的曲面,而是一個帶邊界的曲面(Henle 1994,第 110 頁)。
莫比烏斯帶具有尤拉示性數  (Dodson and Parker 1997, p. 125)。
(Dodson and Parker 1997, p. 125)。
根據 Madachy (1979) 的說法,B. F. Goodrich 公司獲得了一種莫比烏斯帶形式的傳送帶的專利,這種傳送帶的壽命是傳統傳送帶的兩倍。M. C. 埃舍爾喜歡描繪莫比烏斯帶,它們出現在他的木刻作品《莫比烏斯帶 I》和《莫比烏斯帶 II(紅螞蟻)》中(Bool 等人 1982,第 324 頁;Forty 2003,圖版 70)。
半寬為  的莫比烏斯帶,其中圓心半徑為
的莫比烏斯帶,其中圓心半徑為  且高度為
且高度為  可以引數化表示為
可以引數化表示為
對於 ![s in [-w,w]](/images/equations/MoebiusStrip/Inline14.svg) 和
和  。在這種引數化中,莫比烏斯帶因此是一個三次曲面,其方程為
。在這種引數化中,莫比烏斯帶因此是一個三次曲面,其方程為
 |
(4)
|
上面的圖示顯示了沿著莫比烏斯帶長度方向相互齧合的轉動齒輪(M. Trott,私人通訊,2001)。
這個曲面的第一基本形式的係數是
第二基本形式的係數是
面積元素是
 |
(11)
|
並且高斯和平均曲率是
莫比烏斯帶的周長是透過積分複雜函式給出的
![ds=sqrt(x^('2)+y^('2))
=[1/(16)w^4cos^4(1/2t)+{[R+wcos(1/2t)]cost-1/2wsin(1/2t)sint}^4+{Rsint+1/4w[sin(1/2t)+3sin(3/2t)]}^4]^(1/2)](/images/equations/MoebiusStrip/NumberedEquation3.svg) |
(14)
|
從 0 到  的積分,遺憾的是無法以閉合形式完成。請注意,雖然曲面在
的積分,遺憾的是無法以閉合形式完成。請注意,雖然曲面在  處閉合,但這對應於底部邊緣與頂部邊緣連線,如上圖所示,因此必須額外遍歷
處閉合,但這對應於底部邊緣與頂部邊緣連線,如上圖所示,因此必須額外遍歷  才能構成邊界邊緣的整個弧長。
才能構成邊界邊緣的整個弧長。
切割莫比烏斯帶,給它額外的扭曲,然後重新連線兩端會產生意想不到的圖形,稱為併合環(Listing 和 Tait 1847,Ball 和 Coxeter 1987),如下表所示。
| 半扭曲 | 切割 | 分段 | 結果 |
| 1 | 1 | 2 | 1 條帶,長度 2 |
| 1 | 1 | 3 | 1 條帶,長度 2 |
| | | 1 條莫比烏斯帶,長度 1 |
| 1 | 2 | 4 | 2 條帶,長度 2 |
| 1 | 2 | 5 | 2 條帶,長度 2 |
| | | 1 條莫比烏斯帶,長度 1 |
| 1 | 3 | 6 | 3 條帶,長度 2 |
| 1 | 3 | 7 | 3 條帶,長度 2 |
| | | 1 條莫比烏斯帶,長度 1 |
| 2 | 1 | 2 | 2 條帶,長度 1 |
| 2 | 2 | 3 | 3 條帶,長度 1 |
| 2 | 3 | 4 | 4 條帶,長度 1 |
一個環面可以被切割成具有偶數個半扭曲的莫比烏斯帶,一個克萊因瓶可以沿著其長度方向對半切割以製成兩條莫比烏斯帶。此外,當解開時,兩個彼此疊加的條帶,每個條帶都具有半扭曲,會形成一個具有四個扭曲的條帶。
沿著邊界將莫比烏斯帶連線到圓盤的拓撲結果是一個實射影平面,它不能嵌入到  中。然而,有三個曲面是在
中。然而,有三個曲面是在  中實射影平面的表示,具有自相交,即博伊曲面、交叉帽和羅馬曲面。
中實射影平面的表示,具有自相交,即博伊曲面、交叉帽和羅馬曲面。
莫比烏斯帶上的任何區域集合都可以僅使用六種顏色著色,如上面的Tietze 圖所示。
另請參閱
博伊曲面,
交叉帽,
地圖著色,
莫比烏斯帶剖分,
不可定向曲面,
併合環,
稜柱環,
羅馬曲面,
Tietze 圖 在 課堂中探索此主題
使用 探索
參考文獻
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, pp. 127-128, 1987.Bogomolny, A. "Möbius Strip." http://www.cut-the-knot.org/do_you_know/moebius.shtml.Bondy, J. A. and Murty, U. S. R. Graph Theory with Applications. New York: North Holland, p. 243, 1976.Bool, F. H.; Kist, J. R.; Locher, J. L.; and Wierda, F. M. C. Escher: His Life and Complete Graphic Work. New York: Abrams, 1982.Derbyshire, J. Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York: Penguin, 2004. Dickau, R. "Spinning Möbius Strip Movie." http://mathforum.org/advanced/robertd/moebius.htmlDodson, C. T. J. and Parker, P. E. A User's Guide to Algebraic Topology. Dordrecht, Netherlands: Kluwer, pp. 121 and 284, 1997.Escher, M. C. "Moebius Strip I." Wood engraving and woodcut in red, green, gold and black, printed from 4 blocks. 1961. http://www.mcescher.com/Gallery/recogn-bmp/LW437.jpg.Escher, M. C. "Moebius Strip II (Red Ants)." Woodcut in red, black and grey-green, printed from 3 blocks. 1963. http://www.mcescher.com/Gallery/recogn-bmp/LW441.jpg.Forty, S. M.C. Escher. Cobham, England: TAJ Books, 2003.Gardner, M. "Möbius Bands." Ch. 9 in Mathematical Magic Show: More Puzzles, Games, Diversions, Illusions and Other Mathematical Sleight-of-Mind from Scientific American. New York: Vintage, pp. 123-136, 1978.Gardner, M. The Sixth Book of Mathematical Games from Scientific American. Chicago, IL: University of Chicago Press, p. 10, 1984.Geometry Center. "The Möbius Band." http://www.geom.umn.edu/zoo/features/mobius/.Gray, A. "The Möbius Strip." §14.3 in Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed. Boca Raton, FL: CRC Press, pp. 325-326, 1997.Henle, M. A Combinatorial Introduction to Topology. New York: Dover, p. 110, 1994.Hunter, J. A. H. and Madachy, J. S. Mathematical Diversions. New York: Dover, pp. 41-45, 1975.JavaView. "Classic Surfaces from Differential Geometry: Moebius Strip." http://www-sfb288.math.tu-berlin.de/vgp/javaview/demo/surface/common/PaSurface_MoebiusStrip.html.Kraitchik, M. §8.4.3 in Mathematical Recreations. New York: W. W. Norton, pp. 212-213, 1942.Listing and Tait. Vorstudien zur Topologie, Göttinger Studien, Pt. 10, 1847.Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, p. 7, 1979.Möbius, A. F. Werke, Vol. 2. p. 519, 1858.Nordstrand, T. "Moebiusband." http://jalape.no/math/moebtxt.Pappas, T. "The Moebius Strip & the Klein Bottle," "A Twist to the Moebius Strip," "The 'Double' Moebius Strip." The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, p. 207, 1989.Pickover, C. A. The Möbius Strip: Dr. August Mobius's Marvelous Band in Mathematics, Games, Literature, Art, Technology, and Cosmology. New York: Thunder's Mouth Press, 2006.Steinhaus, H. Mathematical Snapshots, 3rd ed. New York: Dover, pp. 269-274, 1999.Trott, M. "The Mathematica Guidebooks Additional Material: Rotating Möbius Bands." http://www.mathematicaguidebooks.org/additions.shtml#G_2_01.Underwood, M. "Mobius Scarf, Klein Bottle, Klein Bottle 'Hat'." http://www.woolworks.org/patterns/klein.txt.Wagon, S. "Rotating Circles to Produce a Torus or Möbius Strip." §7.4 in Mathematica in Action. New York: W. H. Freeman, pp. 229-232, 1991.
Dickau, R. "Spinning Möbius Strip Movie." http://mathforum.org/advanced/robertd/moebius.htmlDodson, C. T. J. and Parker, P. E. A User's Guide to Algebraic Topology. Dordrecht, Netherlands: Kluwer, pp. 121 and 284, 1997.Escher, M. C. "Moebius Strip I." Wood engraving and woodcut in red, green, gold and black, printed from 4 blocks. 1961. http://www.mcescher.com/Gallery/recogn-bmp/LW437.jpg.Escher, M. C. "Moebius Strip II (Red Ants)." Woodcut in red, black and grey-green, printed from 3 blocks. 1963. http://www.mcescher.com/Gallery/recogn-bmp/LW441.jpg.Forty, S. M.C. Escher. Cobham, England: TAJ Books, 2003.Gardner, M. "Möbius Bands." Ch. 9 in Mathematical Magic Show: More Puzzles, Games, Diversions, Illusions and Other Mathematical Sleight-of-Mind from Scientific American. New York: Vintage, pp. 123-136, 1978.Gardner, M. The Sixth Book of Mathematical Games from Scientific American. Chicago, IL: University of Chicago Press, p. 10, 1984.Geometry Center. "The Möbius Band." http://www.geom.umn.edu/zoo/features/mobius/.Gray, A. "The Möbius Strip." §14.3 in Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed. Boca Raton, FL: CRC Press, pp. 325-326, 1997.Henle, M. A Combinatorial Introduction to Topology. New York: Dover, p. 110, 1994.Hunter, J. A. H. and Madachy, J. S. Mathematical Diversions. New York: Dover, pp. 41-45, 1975.JavaView. "Classic Surfaces from Differential Geometry: Moebius Strip." http://www-sfb288.math.tu-berlin.de/vgp/javaview/demo/surface/common/PaSurface_MoebiusStrip.html.Kraitchik, M. §8.4.3 in Mathematical Recreations. New York: W. W. Norton, pp. 212-213, 1942.Listing and Tait. Vorstudien zur Topologie, Göttinger Studien, Pt. 10, 1847.Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, p. 7, 1979.Möbius, A. F. Werke, Vol. 2. p. 519, 1858.Nordstrand, T. "Moebiusband." http://jalape.no/math/moebtxt.Pappas, T. "The Moebius Strip & the Klein Bottle," "A Twist to the Moebius Strip," "The 'Double' Moebius Strip." The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, p. 207, 1989.Pickover, C. A. The Möbius Strip: Dr. August Mobius's Marvelous Band in Mathematics, Games, Literature, Art, Technology, and Cosmology. New York: Thunder's Mouth Press, 2006.Steinhaus, H. Mathematical Snapshots, 3rd ed. New York: Dover, pp. 269-274, 1999.Trott, M. "The Mathematica Guidebooks Additional Material: Rotating Möbius Bands." http://www.mathematicaguidebooks.org/additions.shtml#G_2_01.Underwood, M. "Mobius Scarf, Klein Bottle, Klein Bottle 'Hat'." http://www.woolworks.org/patterns/klein.txt.Wagon, S. "Rotating Circles to Produce a Torus or Möbius Strip." §7.4 in Mathematica in Action. New York: W. H. Freeman, pp. 229-232, 1991. Wang, P. "Renderings." http://www.ugcs.caltech.edu/~peterw/portfolio/renderings/Wells, D. The Penguin Dictionary of Curious and Interesting Geometry. London: Penguin, pp. 152-153 and 164, 1991.
Wang, P. "Renderings." http://www.ugcs.caltech.edu/~peterw/portfolio/renderings/Wells, D. The Penguin Dictionary of Curious and Interesting Geometry. London: Penguin, pp. 152-153 and 164, 1991.
請引用為
Weisstein, Eric W. "莫比烏斯帶。" 來自 -- 資源。 https://mathworld.tw/MoebiusStrip.html
主題分類
(Dodson and Parker 1997, p. 125)。
的莫比烏斯帶,其中圓心半徑為
且高度為
可以引數化表示為
和
。在這種引數化中,莫比烏斯帶因此是一個三次曲面,其方程為
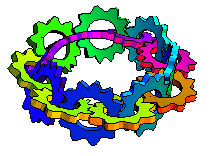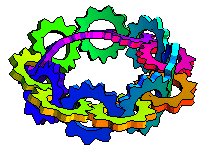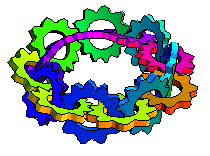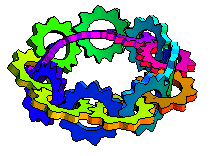
![R/(sqrt(4R^2+3s^2+2s[4Rcos(1/2t)+scost]))](/images/equations/MoebiusStrip/Inline30.svg)
![([2(R^2+s^2)+4Rscos(1/2t)+s^2cost]sin(1/2t))/(sqrt(4R^2+3s^2+2s[4Rcos(1/2t)+scost])),](/images/equations/MoebiusStrip/Inline33.svg)
![-(4R^2)/({4R^2+3s^2+2s[4Rcos(1/2t)+scost]}^2)](/images/equations/MoebiusStrip/Inline36.svg)
![(2[2(R^2+s^2)+4Rscos(1/2t)+s^2cost]sin(1/2t))/({4R^2+3s^2+2s[4Rcos(1/2t)+scost]}^2).](/images/equations/MoebiusStrip/Inline39.svg)
![ds=sqrt(x^('2)+y^('2))
=[1/(16)w^4cos^4(1/2t)+{[R+wcos(1/2t)]cost-1/2wsin(1/2t)sint}^4+{Rsint+1/4w[sin(1/2t)+3sin(3/2t)]}^4]^(1/2)](/images/equations/MoebiusStrip/NumberedEquation3.svg)
的積分,遺憾的是無法以閉合形式完成。請注意,雖然曲面在
處閉合,但這對應於底部邊緣與頂部邊緣連線,如上圖所示,因此必須額外遍歷
才能構成邊界邊緣的整個弧長。
中。然而,有三個曲面是在
中實射影平面的表示,具有自相交,即博伊曲面、交叉帽和羅馬曲面。