主題
Search

羅馬曲面

下載 Mathematica 筆記本下載 Wolfram 筆記本
RomanSurface

羅馬曲面，也稱為 Steiner 曲面（不要與 Steiner 曲面 類混淆，羅馬曲面是 Steiner 曲面類的一個特例），是一種 四次 不可定向曲面。羅馬曲面是透過將 莫比烏斯帶縫合到 圓盤的邊緣而獲得的三種可能的曲面之一。另外兩種是 Boy 曲面 和 交叉帽，所有這些都與 實射影平面 同胚 (Pinkall 1986)。

羅馬曲面的中心點是一個普通的 三重點，具有 (+/-1,0,0)=(0,+/-1,0)=(0,0,+/-1)，並且三條自相交線的六個端點是奇異 夾點，也稱為 夾點。羅馬曲面本質上是由六個粘在一起的 交叉帽 組成，幷包含雙 無窮 個 圓錐曲線。

羅馬曲面可以由以下方程給出

(x^2+y^2+z^2-k^2)^2=[(z-k)^2-2x^2][(z+k)^2-2y^2].
(1)

求解 z 得到方程組

z=(k(y^2-x^2)+/-(x^2-y^2)sqrt(k^2-x^2-y^2))/(2(x^2+y^2)).
(2)

如果曲面繞 z 軸 旋轉 45 度，透過 旋轉矩陣

R_z(45 degrees)=1/(sqrt(2))[1 1 0; -1 1 0; 0 0 1]
(3)

得到

[x^'; y^'; z^']=R_z(45 degrees)[x; y; z],
(4)

那麼簡單的方程

x^2y^2+x^2z^2+y^2z^2+2kxyz=0
(5)

結果。

羅馬曲面也可以使用 不可定向曲面 的通用方法生成，使用多項式函式

f(x,y,z)=a(xy,yz,zx)
(6)

(Pinkall 1986)。設定

x=cosusinv
(7)
y=sinusinv
(8)
z=cosv
(9)

在前一個式子中得到

x(u,v)=1/2asin(2u)sin^2v
(10)
y(u,v)=1/2asinucos(2v)
(11)
z(u,v)=1/2acosusin(2v)
(12)

對於 u 在 [0,2pi) 中 和 v 在 [-pi/2,pi/2] 中。這給出了代數方程

x^2y^2+x^2z^2+y^2z^2-axyz=0,
(13)

對應於上述通用方程中的 a=-2k。 第一基本形式 和 第二基本形式 的係數稍微複雜，高斯曲率和平均曲率也是如此。所圍成的 體積 由下式給出

V=1/6a^3,
(14)

其慣性矩張量為

I=[1/(10)Ma^2 0 0; 0 1/(10)Ma^2 0; 0 0 1/(10)Ma^2].
(15)
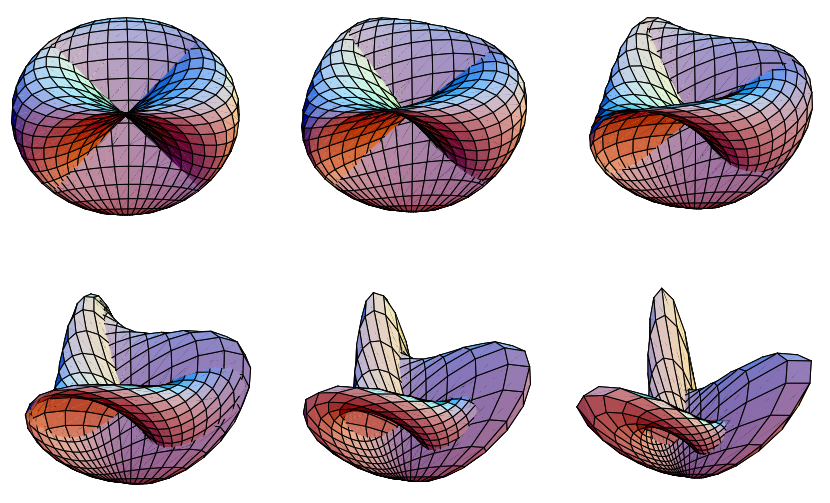
RomanBoy

羅馬曲面和 Boy 曲面 之間的 同倫（平滑變形）由以下方程給出

x(u,v)=(sqrt(2)cos(2u)cos^2v+cosusin(2v))/(2-alphasqrt(2)sin(3u)sin(2v))
(16)
y(u,v)=(sqrt(2)sin(2u)cos^2v-sinusin(2v))/(2-alphasqrt(2)sin(3u)sin(2v))
(17)
z(u,v)=(3cos^2v)/(2-alphasqrt(2)sin(3u)sin(2v))
(18)

對於 u 在 [-pi/2,pi/2] 中 和 v 在 [0,pi] 中，當 alpha 從 0 變為 1 時。alpha=0 對應於羅馬曲面，alpha=1 對應於 Boy 曲面。

參見

Boy 曲面, 交叉帽, 七面體, 莫比烏斯帶, 不可定向曲面, 四次曲面, Steiner 曲面

使用 探索

參考文獻

Dharwadker, A. "Heptahedron and Roman Surface." Electronic Geometry Model No. 2003.05.001. http://www.eg-models.de/models/Surfaces/Algebraic_Surfaces/2003.05.001/.Fischer, G. (Ed.). Mathematische Modelle aus den Sammlungen von Universitäten und Museen, Kommentarband. Braunschweig, Germany: Vieweg, p. 19, 1986.Fischer, G. (Ed.). Plates 42-44 and 108-114 in Mathematische Modelle aus den Sammlungen von Universitäten und Museen, Bildband. Braunschweig, Germany: Vieweg, pp. 42-44 and 108-109, 1986.Geometry Center. "The Roman Surface." http://www.geom.umn.edu/zoo/toptype/pplane/roman/.Gray, A. "Steiner's Roman Surface." Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed. Boca Raton, FL: CRC Press, pp. 331-333, 1997.Nordstrand, T. "Steiner's Roman Surface." http://jalape.no/math/steintxt.Pinkall, U. Mathematical Models from the Collections of Universities and Museums (Ed. G. Fischer). Braunschweig, Germany: Vieweg, p. 64, 1986.更新連結Wang, P. "Renderings." http://www.ugcs.caltech.edu/~peterw/portfolio/renderings/

請引用為

Weisstein, Eric W. "羅馬曲面." 來自 Web 資源. https://mathworld.tw/RomanSurface.html

主題分類