謝爾賓斯基篩法

謝爾賓斯基篩法是由謝爾賓斯基於 1915 年描述的一種分形，在 13 世紀的義大利藝術中就已出現 (Wolfram 2002, p. 43)。它也被稱為謝爾賓斯基墊片或謝爾賓斯基三角形。該曲線可以寫成 Lindenmayer 系統，初始字串為"FXF--FF--FF", 字串重寫 規則"F" -> "FF", "X" -> "--FXF++FXF++FXF--", 和角度 .

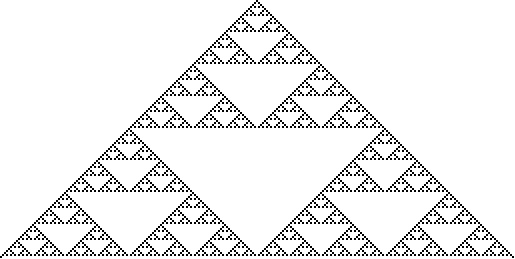
謝爾賓斯基篩法的第 次迭代在 Wolfram Language 中實現為SierpinskiMesh[n].

設 為迭代 後黑色三角形的數量， 為三角形邊的長度， 為第 次迭代後黑色的 面積 分數。則

			(1)
			(2)
			(3)

因此，容量維度為

			(4)
			(5)
			(6)
			(7)

(OEIS A020857; Wolfram 1984; Borwein and Bailey 2003, p. 46).

謝爾賓斯基篩法由美麗的遞推方程產生

(8)

其中 表示按位 異或。它也由下式給出

(9)

其中 是由下式定義的第 個最低有效位

(10)

並且乘積取遍所有滿足 的 (Allouche and Shallit 2003, p. 113)。

謝爾賓斯基篩法由 帕斯卡三角形 (mod 2) 給出，給出序列 1; 1, 1; 1, 0, 1; 1, 1, 1, 1; 1, 0, 0, 0, 1; ... (OEIS A047999; 左圖)。換句話說，在帕斯卡三角形中，將所有奇數著色為黑色，將偶數著色為白色，會產生謝爾賓斯基篩法 (Guy 1990; Wolfram 2002, p. 870; 中圖)。二項式係數 mod 2 可以使用按位運算 AND(NOT(), ) 計算，給出序列 0; 0, 0; 0, 1, 0; 0, 0, 0, 0; 0, 1, 2, 3, 0; ... (OEIS A102037; 右圖)，然後如果結果為 0 則將三角形著色為黑色，否則著色為白色。這是 盧卡斯對應定理 對於二項式係數模素數的推論。

令人驚訝的是，基本元胞自動機規則 60、90 和 102 (當省略尾隨零時) 也產生謝爾賓斯基篩法 (Wolfram 2002, p. 870)。Wolfram (2002, pp. 931-932) 給出了大量可用於計算謝爾賓斯基篩法的演算法。

Gardner (1977) 和 Watkins (Conway 和 Guy 1996, Krížek et al. 2001) 獨立注意到，邊數為奇數的可構造多邊形的邊數由謝爾賓斯基篩法的前 32 行解釋為 二進位制數給出，給出 1, 3, 5, 15, 17, 51, 85, 255, ... (OEIS A004729, Conway 和 Guy 1996, p. 140)。換句話說，每一行都是不同費馬素數的乘積，項由二進位制計數給出。