參見
Barnsley 蕨葉,
謝爾賓斯基篩
使用 探索
參考文獻
Borwein, J. 和 Bailey, D. “帕斯卡三角形。” §2.1 in Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, pp. 47-48, 2003.Barnsley, M. F. 和 Rising, H. Fractals Everywhere, 2nd ed. Boston, MA: Academic Press, 1993.Bogomolny, A. “謝爾賓斯基墊片與混沌遊戲。” http://www.cut-the-knot.org/Curriculum/Geometry/SierpinskiChaosGame.shtml.Dickau, R. M. “混沌遊戲。” http://mathforum.org/advanced/robertd/chaos_game.html.Jeffrey, H. J. “遺傳序列的混沌遊戲表示。” Nucleic Acids Res. 18, 2163-2170, 1990.Jeffrey, H. J. “序列的混沌遊戲視覺化。” Comput. & Graphics 16, 25-33, 1992. Reprinted in Chaos and Fractals, A Computer Graphical Journey: Ten Year Compilation of Advanced Research (Ed. C. A. Pickover). Amsterdam, Netherlands: Elsevier, pp. 5-13, 1998.Peitgen, H.-O.; Jürgens, H.; 和 Saupe, D. Fractals for the Classroom, Part 1: Introduction to Fractals and Chaos. New York: Springer-Verlag, pp. 41-43, 1992.Pickover, C. A. (編.). Fractal Horizons: The Future Use of Fractals. New York: St. Martin's Press, pp. 27, 57-59, and 169-171, 1996.Wagon, S. Mathematica in Action, 2nd ed. New York: Springer-Verlag, pp. 226-239, 1999.在 上被引用
混沌遊戲
請這樣引用本文
Weisstein, Eric W. “混沌遊戲。” 來自 網路資源。 https://mathworld.tw/ChaosGame.html
主題分類
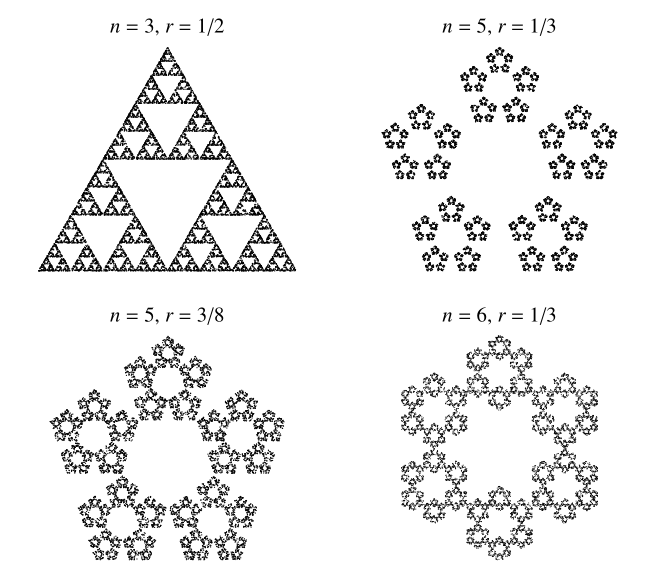
邊形內隨機選擇一個點。然後繪製下一個點,該點與隨機選擇的多邊形頂點之間的距離為
分之一。繼續這個過程(在丟棄最初的幾個點之後)。這個“混沌遊戲”的結果有時是,但並非總是,一個分形。上面顯示了針對幾個
值的混沌遊戲結果。

個點,且
時的混沌遊戲。案例
給出了正方形的內部,所有點被訪問的機率均等。
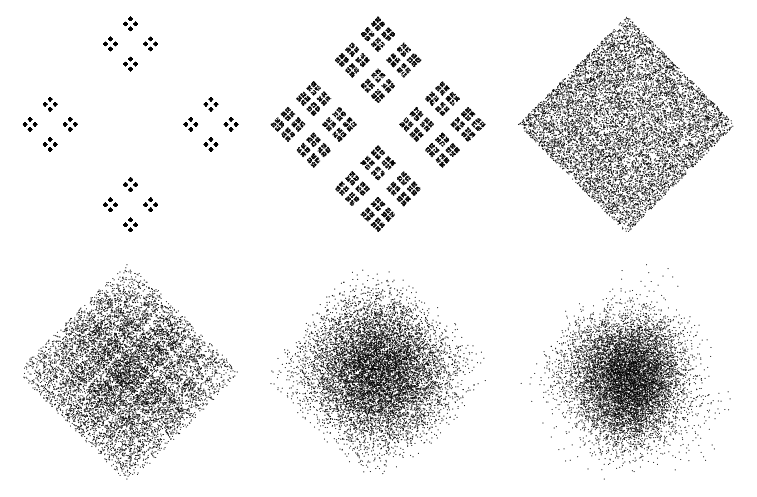
個點,且
、0.4、0.5、0.6、0.75 和 0.9 時的混沌遊戲。