大二十面體

大二十面體，不要與大icosidodecahedron或大icosicosidodecahedron混淆，是開普勒-泊松多面體，其對偶是大星形十二面體。它也是 Maeder 索引為 53 (Maeder 1997)、Wenninger 索引為 41 (Wenninger 1989)、Coxeter 索引為 69 (Coxeteret al.1954) 和 Har'El 索引為 58 (Har'El 1993) 的均勻多面體。它具有Schläfli 符號 和Wythoff 符號 。

大二十面體可以從邊長為單位長度的二十面體構建，方法是取 20 組頂點，這些頂點彼此間隔距離 ，即黃金比例。因此，該實體由 20 個等邊三角形組成。它們的排列方式的對稱性使得所得實體包含 12 個五角星。

最容易構建大二十面體的方法是，從相應的網格（左上圖）構建一個“壓扁的”十二面體（右上圖）。然後，使用左下圖所示的網格，構建 12 個五角星錐體（中下圖），並將它們貼在凹坑中（右下圖）。Cundy 和 Rollett (1989, pp. 98-99) 給出了這種構建方法。如果十二面體的邊長為單位長度，則五角星錐體的高度（在十二面體面之上）由求解五角錐體的邊長方程給出

(1)

其中 ，得到

(2)

然後，從十二面體的中心到錐體頂點的距離由下式給出

(3)

其中 是十二面體的內半徑。

大二十面體的骨架與二十面體圖同構。

上面的插圖顯示了一個大二十面體的紙雕。模型的每個面平面都是不同的顏色，但成對的平行面使用相同的顏色。該模型由 180 個部件製成。

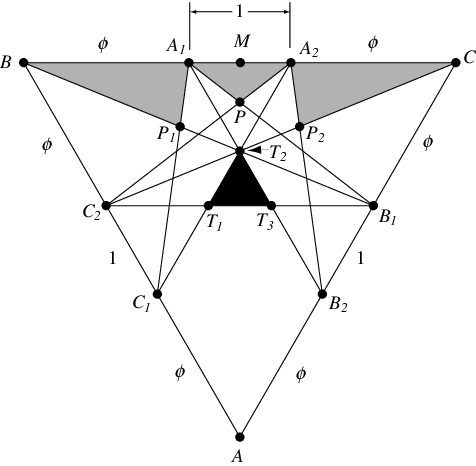
五角星錐體的尺寸可以透過檢查大二十面體的三角形截面來確定。在這個三角形中，每條邊都按比例 分割，並如圖所示繪製線條。然後，左側和右側的淺色陰影部分對應於兩個錐體的側面，中心陰影部分是前兩個錐體之間錐體的“唇”。此外，圖中的填充部分對應於刻在大二十面體中的二十面體的一個面。在上面圖形的符號中，

			(4)
			(5)
			(6)
			(7)
			(8)

由邊長為單位長度的十二面體構建的大二十面體的邊長（其中邊被解釋為在面平面相交處斷開）由下式給出

			(9)
			(10)
			(11)
			(12)

它的外接球半徑是

(13)

然後表面積和體積是

			(14)
			(15)
			(16)

大二十面體的凸包是一個正二十面體，二十面體的對偶是十二面體，所以大二十面體的對偶是十二面體星狀體之一 (Wenninger 1983, p. 40)