外接圓

給定一個三角形，將兩條邊沿其公共頂點的相反方向延伸。與這兩條直線以及三角形的另一邊相切的圓稱為外接圓，有時也稱為旁切圓。圓心 被稱為外心，位於對面角的外角平分線上。每個三角形都有三個外接圓，外心的三線座標為 , , 和 。半徑 外接圓 被稱為其外半徑。

請注意，三個外接圓不一定與內切圓相切，因此這四個圓不等同於索迪圓的配置。

沒有 Kimberling 中心位於任何外接圓上。

給定一個三角形，其內半徑為 ，令 為外接圓的高度， 為它們的半徑（外半徑）。那麼

(Johnson 1929, p. 189).

有四個圓與給定三角形的所有三條邊（或其延長線）相切：內切圓 和三個外接圓 , , 和 。這四個圓反過來都與九點圓 相切。內切圓在費爾巴哈點 與九點圓相切，與外接圓的切點形成費爾巴哈三角形。

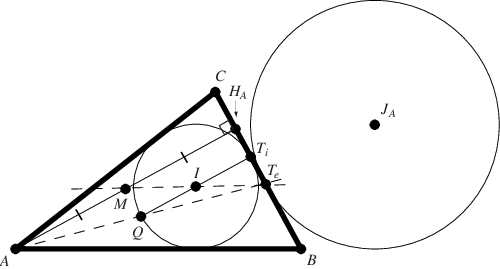
給定一個三角形 ，構造內切圓，其內心為 ，以及外接圓，其外心為 。令 為 與其內切圓的切點， 為 與其外接圓 的切點， 為頂點 的高度的垂足， 為 的中點，並構造 ，使得 是內切圓的直徑。那麼 , , 和 是共線的，, , 和 也是共線的 (Honsberger 1995)。