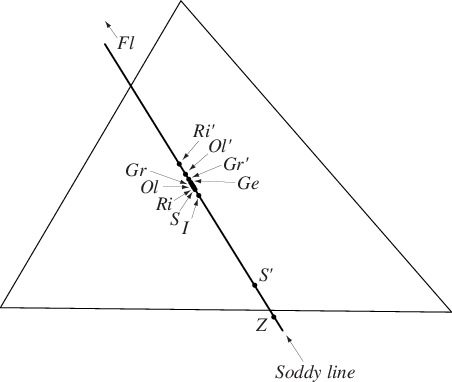
索迪線是中心線 並且具有三線方程
它穿過 Kimberling 中心 ,對於
( 內心
), 7 ( 格爾貢點 Ge ), 20 ( de Longchamps 點
), 77, 170, 175 ( 外索迪中心
), 176 ( 內索迪中心
), 269, 279, 347, 390, 481 ( 第一 Eppstein 點 ), 482 ( 第二 Eppstein 點 ), 962 (Longuet-Higgins 點), 990, 991, 1042, 1044, 1323 ( Fletcher 點 Fl ), 1371 (內 Rigby 點
), 1372 (外 Rigby 點
), 1373 (內 Griffiths 點
), 1374 (外 Griffiths 點
), 1442, 1443, 1448, 1458, 1721, 1742, 1770, 2263, 2293, 2951, 3000, 3007, 3010, 3012, 和 3019。
點 ,
,
, 和 Ge 在索迪線上形成一個調和比 (Vandeghen 1964, Oldknow 1996)。在這些 10 個點中,共有 22 個由四個點組成的調和比集合 (Oldknow 1996)。索迪線與尤拉線交於de Longchamps 點,與格爾貢線交於Fletcher 點。此外,索迪線和格爾貢線是垂直的 (Oldknow 1996)。
索迪線是GEOS 圓和尤拉-格爾貢-索迪圓的根軸。
垂足軸和格爾貢線之間的角度等於尤拉線和索迪線之間的角度 (F. Jackson, 私人通訊, 2005 年 11 月 2 日)。