球諧函式  是 拉普拉斯方程 在 球座標系 中當不存在方位角對稱性時的解的角度部分。在識別所使用的符號約定方面必須謹慎。在本條目中,
是 拉普拉斯方程 在 球座標系 中當不存在方位角對稱性時的解的角度部分。在識別所使用的符號約定方面必須謹慎。在本條目中, 被視為極(餘緯)座標,其中
被視為極(餘緯)座標,其中 ![theta in [0,pi]](/images/equations/SphericalHarmonic/Inline3.svg) ,而
,而  被視為方位角(經度)座標,其中
被視為方位角(經度)座標,其中  。這是物理學中常用的約定,正如 Arfken (1985) 和 Wolfram 語言 所描述的那樣(在數學文獻中,
。這是物理學中常用的約定,正如 Arfken (1985) 和 Wolfram 語言 所描述的那樣(在數學文獻中, 通常表示經度座標,而
通常表示經度座標,而  表示餘緯座標)。球諧函式在 Wolfram 語言 中實現為SphericalHarmonicY[l, m, theta, phi].
表示餘緯座標)。球諧函式在 Wolfram 語言 中實現為SphericalHarmonicY[l, m, theta, phi].
球諧函式滿足 球諧微分方程,該方程由 拉普拉斯方程 在 球座標系 中的角度部分給出。在這個方程中寫入  得到
得到
 |
(1)
|
乘以  得到
得到
![[(sintheta)/(Theta(theta))d/(dtheta)(sintheta(dTheta)/(dtheta))+l(l+1)sin^2theta]+1/(Phi(phi))(d^2Phi(phi))/(dphi^2)=0.](/images/equations/SphericalHarmonic/NumberedEquation2.svg) |
(2)
|
使用 分離變數法,透過將  相關部分等同於常數,得到
相關部分等同於常數,得到
 |
(3)
|
其解為
 |
(4)
|
將 (3) 代入 (2) 得到  相關部分的方程,其解為
相關部分的方程,其解為
 |
(5)
|
其中  ,
,  , ..., 0, ...,
, ..., 0, ...,  ,
,  且
且  是一個 締合勒讓德多項式。然後透過組合
是一個 締合勒讓德多項式。然後透過組合  和
和  定義球諧函式,
定義球諧函式,
 |
(6)
|
其中選擇歸一化使得
 |
(7)
|
(Arfken 1985, p. 681)。這裡, 表示 複共軛,而
表示 複共軛,而  是 克羅內克 delta。有時(例如,Arfken 1985),Condon-Shortley 相位
是 克羅內克 delta。有時(例如,Arfken 1985),Condon-Shortley 相位  被預先新增到球諧函式的定義中。
被預先新增到球諧函式的定義中。
球諧函式有時會分為它們的 實部 和 虛部,
 |
(8)
|
 |
(9)
|
球諧函式服從
其中  是 勒讓德多項式。
是 勒讓德多項式。
球諧函式的積分由下式給出
 |
(13)
|
其中  是一個 維格納 3j 符號(它與 克萊佈施-戈爾丹係數 相關)。特殊情況包括
是一個 維格納 3j 符號(它與 克萊佈施-戈爾丹係數 相關)。特殊情況包括
(Arfken 1985, p. 700)。
以上圖示顯示了  (頂部),
(頂部),![R[Y_l^m(theta,phi)]^2](/images/equations/SphericalHarmonic/Inline46.svg) (左下),和
(左下),和 ![I[Y_l^m(theta,phi)]^2](/images/equations/SphericalHarmonic/Inline47.svg) (右下)。前幾個球諧函式是
(右下)。前幾個球諧函式是
用 笛卡爾座標系 表示,
因此
帶諧函式 被定義為 形式為
 |
(43)
|
扇諧函式 是 形式為
 |
(44)
|
 |
(45)
|
對於  。節諧函式 是 形式為
。節諧函式 是 形式為
 |
(46)
|
 |
(47)
|
另請參閱
締合勒讓德多項式,
Condon-Shortley 相位,
相關係數,
拉普拉斯級數,
節諧函式,
實體諧函式,
球諧函式加法定理,
球諧微分方程,
球諧函式閉包關係,
面諧函式,
扇諧函式,
向量球諧函式,
帶諧函式
相關 Wolfram 網站
http://functions.wolfram.com/Polynomials/SphericalHarmonicY/,
http://functions.wolfram.com/HypergeometricFunctions/SphericalHarmonicYGeneral/
使用 探索
參考文獻
Abbott, P. "2. 薛定諤方程。" 計算物理 2 講義。 http://physics.uwa.edu.au/pub/Computational/CP2/2.Schroedinger.nb.Arfken, G. "球諧函式" 和 "三個球諧函式乘積的積分。" §12.6 和 12.9 在 物理學家的數學方法,第 3 版。 奧蘭多,佛羅里達州:學術出版社,pp. 680-685 和 698-700, 1985.Byerly, W. E. "球諧函式。" 第 6 章 在 傅立葉級數、球諧函式、柱諧函式和橢球諧函式的基本論著,附帶在數學物理問題中的應用。 紐約:多佛出版社,pp. 195-218, 1959.Ferrers, N. M. 關於球諧函式及與其相關主題的初等論著。 倫敦:麥克米倫出版社,1877.Groemer, H. 傅立葉級數和球諧函式的幾何應用。 紐約:劍橋大學出版社,1996.Hobson, E. W. 球諧函式和橢球諧函數理論。 紐約:切爾西出版社,1955.Kalf, H. "關於任意維度函式按球諧函式展開。" Bull. Belg. Math. Soc. Simon Stevin 2, 361-380, 1995.MacRobert, T. M. 和 Sneddon, I. N. 球諧函式:調和函式的初等論著,附帶應用,第 3 版修訂版。 牛津,英格蘭:珀加蒙出版社,1967.Normand, J. M. 李群:量子力學中的旋轉。 阿姆斯特丹,荷蘭:北荷蘭,1980.Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; 和 Vetterling, W. T. "球諧函式。" §6.8 在 FORTRAN 數值食譜:科學計算的藝術,第 2 版。 劍橋,英格蘭:劍橋大學出版社,pp. 246-248, 1992.Sansone, G. "調和多項式和球諧函式"、"球諧函式的積分性質和勒讓德多項式的加法定理" 以及 "關於平方可積函式的球諧函式的完備性。" §3.18-3.20 在 正交函式,修訂英文版。 紐約:多佛出版社,pp. 253-272, 1991.Sternberg, W. 和 Smith, T. L. 勢論和球諧函數理論,第 2 版。 多倫多:多倫多大學出版社,1946.Wang, J.; Abbott, P.; 和 Williams, J. "原子軌道的視覺化。" http://physics.uwa.edu.au/pub/Orbitals.Weisstein, E. W. "關於球諧函式的書籍。" http://www.ericweisstein.com/encyclopedias/books/SphericalHarmonics.html.Whittaker, E. T. 和 Watson, G. N. "涉及勒讓德函式的拉普拉斯方程的解" 和 "滿足球體表面上指定邊界條件的拉普拉斯方程的解。" §18.31 和 18.4 在 現代分析教程,第 4 版。 劍橋,英格蘭:劍橋大學出版社,pp. 391-395, 1990.Zwillinger, D. 微分方程手冊,第 3 版。 波士頓,馬薩諸塞州:學術出版社,p. 129, 1997.在 中引用
球諧函式
請引用本文為
Weisstein, Eric W. "球諧函式。" 來源 Web 資源。 https://mathworld.tw/SphericalHarmonic.html
主題分類
是 拉普拉斯方程 在 球座標系 中當不存在方位角對稱性時的解的角度部分。在識別所使用的符號約定方面必須謹慎。在本條目中,
被視為極(餘緯)座標,其中
,而
被視為方位角(經度)座標,其中
。這是物理學中常用的約定,正如 Arfken (1985) 和 Wolfram 語言 所描述的那樣(在數學文獻中,
通常表示經度座標,而
表示餘緯座標)。球諧函式在 Wolfram 語言 中實現為SphericalHarmonicY[l, m, theta, phi].
得到
得到
相關部分等同於常數,得到
,
, ..., 0, ...,
,
且
是一個 締合勒讓德多項式。然後透過組合
和
定義球諧函式,


表示 複共軛,而
是 克羅內克 delta。有時(例如,Arfken 1985),Condon-Shortley 相位
被預先新增到球諧函式的定義中。




是 勒讓德多項式。

是一個 維格納 3j 符號(它與 克萊佈施-戈爾丹係數 相關)。特殊情況包括



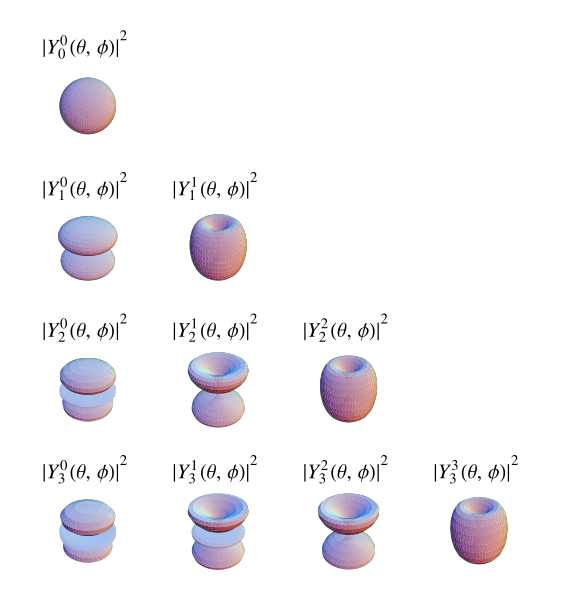
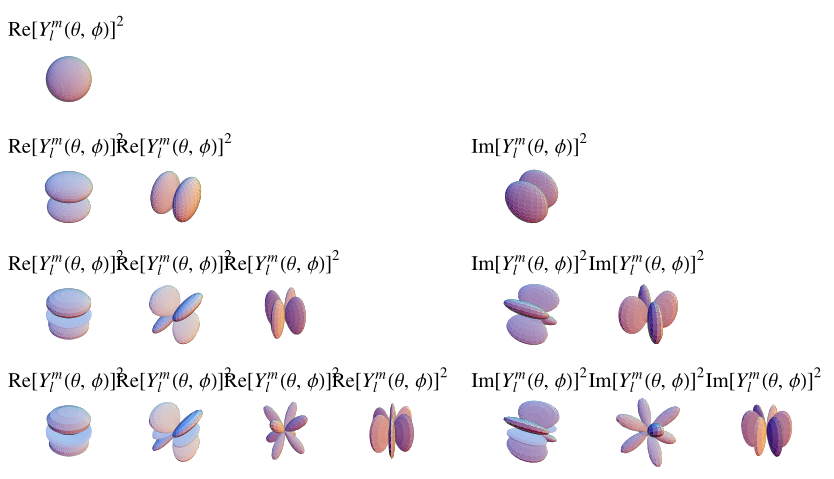
(頂部),
(左下),和
(右下)。前幾個球諧函式是




















