絕對值

最小值 最大值

實數 實數 的絕對值記為 ，定義為 的“無符號”部分，

			(1)
			(2)

其中 是 符號 函式。因此，絕對值始終大於或等於 0。上面繪製了實數 的絕對值（對於實數 ）。

最小值 最大值 Re Im

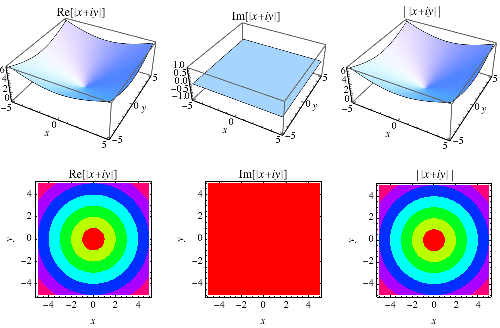複數 的絕對值，也稱為復模，定義為

(3)

此形式在 Wolfram 語言 中實現為Abs[z]，並在上面針對複數 進行了說明。

請注意，導數（讀作：復導數） 不存在，因為在複平面中的每個點， 的導數值都取決於導數方向（因此柯西-黎曼方程不成立）。但是，實導數（即，將導數限制為沿實軸的方向）可以針對 以外的點定義為

(4)

由於諸如 Wolfram 語言 之類的計算機代數語言通常處理復變數（即，導數的定義始終意味著復導數），因此 會被此類軟體正確地返回為未求值。

請注意，符號 通常用於表示復模、p-adic 範數或一般賦值。在這項工作中，向量 的範數也表示為 ，儘管符號 也常見。

向下取整函式 、最近整數函式 和 向上取整函式 的符號與絕對值的符號類似。

兩個變數之差的絕對值的 次冪的單位平方積分由下式給出

(5)

對於 ，當 , 1, ... 時，其值為 1, 1/3, 1/6, 1/10, 1/15, 1/21, ...，即三角數的倒數 (OEIS A000217)，對於 , 2, ...。這種積分出現在卡西米爾效應的研究中（Milton and Ng 1998, eqn. 3.15; Milton 1999, p. 32, eqn. 3.33）。

類似地，對於 ，

(6)

給出 , 1, ... 的前幾個值，分別為 1, 1, 7/6, 3/2, 31, 15, 3, ... (OEIS A116419 和 A116420)。