 |
 |
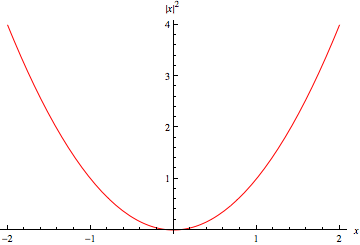
一個複數 的絕對值的平方,也稱為平方範數,定義為
|
(1)
|
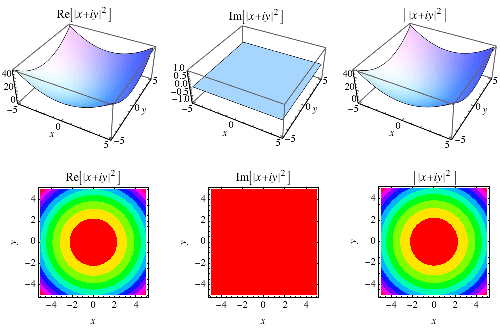
如果複數寫成 ,其中
和
是實數,那麼絕對值的平方可以寫成
|
(2)
|
|
(3)
|
絕對值的平方可以使用 Wolfram 語言 命令根據 和
計算ComplexExpand[Abs[z]^2, TargetFunctions ->
Conjugate
].
一個涉及絕對值的平方的重要恆等式由下式給出
|
(4)
| |||
|
(5)
| |||
|
(6)
|
如果 ,那麼 (6) 變為
|
(7)
| |||
|
(8)
|
如果 ,且
,那麼
|
(9)
|
最後,
|
(10)
| |||
|
(11)
| |||
|
(12)
|