符號函式

最小值 最大值 實部 虛部

實數的符號，也稱為 sgn 或 signum，對於負數（即帶有負號 “”的數）為 ，對於零為 0，對於正數（即帶有正號 “”的數）為 。換句話說，對於實數 ，

(1)

對於實數 ，這可以寫成

(2)

並滿足

(3)

對於實數 也可以定義為

(4)

其中 是 Heaviside 階躍函式。

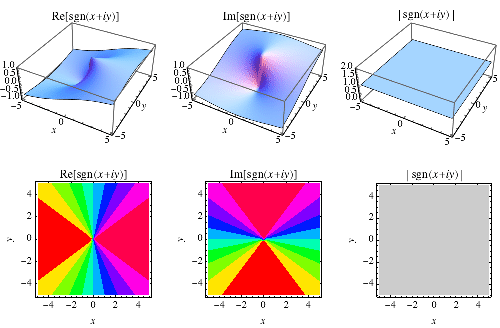
符號函式在 Wolfram 語言 中實現，對於實數 ，表示為符號函式[x]。對於非零複數，符號函式[z] 返回 ，其中 是 的複數模量。

也可以解釋為複平面上單位圓上的未指定點 (Rich and Jeffrey 1996)。