元胞自動機是在指定形狀的網格 上“著色”單元的集合,它根據一組基於相鄰單元狀態的規則,透過若干離散時間步長演化。然後,將這些規則迭代地應用於所需的多個時間步長。馮·諾伊曼是最早考慮這種模型的人之一,並將元胞模型納入了他的“通用構造器”中。在 1950 年代初期,人們研究了元胞自動機,作為生物系統的可能模型(Wolfram 2002,第 48 頁)。S. Wolfram 從 1980 年代開始對元胞自動機進行了全面的研究,Wolfram 在該領域的基礎研究最終促成了他的著作A New Kind of Science (Wolfram 2002)的出版,Wolfram 在書中展示了關於自動機的巨量研究成果,其中包括許多開創性的新發現。
電視劇犯罪劇集數字追兇 Bettor or Worse ”(2006 年)提到了 一維元胞自動機。
元胞自動機有多種形狀和型別。元胞自動機最基本的屬性之一是計算它的網格 型別。最簡單的這種“網格”是一維線。在二維中,可以考慮正方形 、三角形 和六邊形網格 。元胞自動機也可以在任意維數的笛卡爾網格上構建,其中Wolfram 語言 中實現為CellularAutomaton 規則 , 初始狀態 , 步數 ]。
還必須指定元胞自動機可能假設的顏色(或不同狀態)的數量
除了元胞自動機所處的網格及其單元可能假設的顏色之外,還必須指定單元相互影響的鄰域 。最簡單的選擇是“最近鄰域”,其中在每個時間步長隻影響直接相鄰於給定單元的單元。在正方形網格 上的二維元胞自動機的情況下,兩個常見的鄰域是所謂的摩爾鄰域 (正方形鄰域)和馮·諾伊曼鄰域 (菱形鄰域)。
最簡單的元胞自動機型別是二進位制、最近鄰、一維自動機。S. Wolfram 將這種自動機稱為“基本元胞自動機 ”,他廣泛研究了它們驚人的特性(Wolfram 1983;2002,第 57 頁)。共有 256 個這樣的自動機,每個自動機都可以透過唯一的二進位制數進行索引,該二進位制數的十進位制表示形式稱為特定自動機的“規則”。上面顯示了規則 30 的圖示,以及從單個黑色單元開始 15 步後產生的演化。
稍微複雜一點的元胞自動機類別是最近鄰、全域元胞自動機 。在這種自動機中,決定演化的是相鄰單元的平均值 ,最簡單的非平凡示例具有程式碼 912 自動機的規則和 300 步。
在二維中,最著名的元胞自動機是康威的生命遊戲 ,由 J. H. Conway 於 1970 年發現,並在 Martin Gardner 的科學美國人 專欄中普及。生命遊戲 是二進位制(全域元胞自動機 ,具有範圍為摩爾鄰域 。儘管連續生命遊戲 世代的計算最初是手工完成的,但計算機革命很快到來,使得可以研究和傳播更廣泛的模式。上面說明了被稱為充氣火車(puffer train)的生命遊戲 構造的動畫。
線世界 是另一種常見的二維元胞自動機。
元胞自動機的理論非常豐富,簡單的規則和結構能夠產生各種意想不到的行為。例如,存在通用元胞自動機 ,它能夠模擬任何其他元胞自動機或圖靈機 的行為。Gacs (2001) 甚至證明,存在容錯通用元胞自動機,只要擾動足夠稀疏,它們的模擬其他元胞自動機的能力就不會受到隨機擾動的阻礙。
另請參閱 抽象機 ,
自動機理論 ,
程式碼 177 ,
程式碼 912 ,
程式碼 2040 ,
基本元胞自動機 ,
射擊隊問題 ,
生命遊戲 ,
移動自動機 ,
摩爾鄰域 ,
規則 30 ,
規則 60 ,
規則 90 ,
規則 102 ,
規則 110 ,
規則 150 ,
規則 250 ,
全域元胞自動機 ,
圖靈機 ,
通用元胞自動機 ,
馮·諾伊曼鄰域 ,
線世界 在 課堂中探索此主題
在 中探索
參考文獻 Adami, C. Artificial Life. Buchi, J. R. 和 Siefkes, D. (編). Finite Automata, Their Algebras and Grammars: Towards a Theory of Formal Expressions. Burks, A. W. (編). Essays on Cellular Automata. Cipra, B. "Cellular Automata Offer New Outlook on Life, the Universe, and Everything." 在 What's Happening in the Mathematical Sciences, 1995-1996, Vol. 3. Dewdney, A. K. The Armchair Universe: An Exploration of Computer Worlds. Gacs, P. "Reliable Cellular Automata with Self-Organization." J. Stat. Phys. 103 , 45-267, 2001. Gardner, M. "The Game of Life, Parts I-III." 第 20-22 章,在 Wheels, Life, and other Mathematical Amusements. Goles, E. 和 Martínez, S. (編). Cellular Automata and Complex Systems. Gutowitz, H. (編). Cellular Automata: Theory and Experiment. Hopcroft, J. E. 和 Ullman, J. D. Introduction to Automata Theory, Languages, and Computation. Hopcroft J. E. "An The Theory of Machines and Computations Levy, S. Artificial Life: A Report from the Frontier Where Computers Meet Biology. Martin, O.; Odlyzko, A.; 和 Wolfram, S. "Algebraic Aspects of Cellular Automata." Communications in Mathematical Physics 93 , 219-258, 1984. McIntosh, H. V. "Cellular Automata Miscellanea." http://delta.cs.cinvestav.mx/~mcintosh/ . Preston, K. Jr. 和 Duff, M. J. B. Modern Cellular Automata: Theory and Applications. http://library.wolfram.com/infocenter/MathSource/505/ .Sigmund, K. Games of Life: Explorations in Ecology, Evolution and Behaviour. Sloane, N. J. A. 序列 A006977 /M2497 在 "整數序列線上百科全書" 中。 Sloane, N. J. A. 和 Plouffe, S. 圖 M2497 在 The Encyclopedia of Integer Sequences. Toffoli, T. 和 Margolus, N. Cellular Automata Machines: A New Environment for Modeling. Weisstein, E. W. "Books about Cellular Automata." http://www.ericweisstein.com/encyclopedias/books/CellularAutomata.html . Wolfram, S. "Statistical Mechanics of Cellular Automata." Rev. Mod. Phys. 55 , 601-644, 1983. Wolfram, S. "Twenty Problems in the Theory of Cellular Automata." Physica Scripta T9 , 170-183, 1985. Wolfram, S. (編). Theory and Application of Cellular Automata. Wolfram, S. Cellular Automata and Complexity: Collected Papers. Wolfram, S. A New Kind of Science. Wuensche, A. 和 Lesser, M. The Global Dynamics of Cellular Automata: An Atlas of Basin of Attraction Fields of One-Dimensional Cellular Automata. 在 上被引用 元胞自動機
請引用為
Weisstein, Eric W. "元胞自動機。" 來自 https://mathworld.tw/CellularAutomaton.html
學科分類 更多... 更少...
維整數格
是最常見的選擇。在
維整數格上的元胞自動機在 Wolfram 語言中實現為CellularAutomaton[規則, 初始狀態, 步數]。
。這個數字通常是整數,其中
(二進位制)是最簡單的選擇。對於二進位制自動機,顏色 0 通常稱為“白色”,顏色 1 通常稱為“黑色”。但是,也可以考慮具有連續值範圍的元胞自動機。
色、一維全域元胞自動機。在這種自動機中,決定演化的是相鄰單元的平均值,最簡單的非平凡示例具有
種顏色。對於這些自動機,描述行為的規則集可以編碼為
位
進位制數,稱為“程式碼”。上面說明了三元(
)程式碼 912 自動機的規則和 300 步。
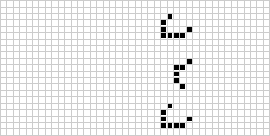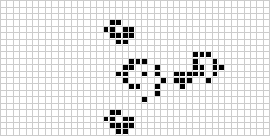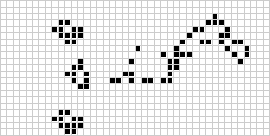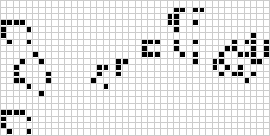
)全域元胞自動機,具有範圍為
的摩爾鄰域。儘管連續生命遊戲世代的計算最初是手工完成的,但計算機革命很快到來,使得可以研究和傳播更廣泛的模式。上面說明了被稱為充氣火車(puffer train)的生命遊戲構造的動畫。