生命遊戲是最著名的二維細胞自動機,由約翰·H·康威發明,並在馬丁·加德納於 1970 年 10 月開始的《科學美國人》專欄中普及。生命遊戲最初是透過手工使用計數器進行(即,產生連續世代),但在計算機上的實現大大提高了探索模式的便利性。
生命細胞自動機的執行方式是在二維網格上放置一些填充的單元格。然後,每一代都會根據周圍單元格的狀態開啟或關閉單元格。規則定義如下。檢查當前單元格周圍的所有八個單元格,看它們是否處於開啟狀態。任何處於開啟狀態的單元格都會被計數,然後使用此計數來確定當前單元格會發生什麼。
1. 死亡:如果計數小於 2 或大於 3,則當前單元格關閉。
2. 生存:如果 (a) 計數正好為 2,或者 (b) 計數正好為 3 且當前單元格處於開啟狀態,則當前單元格保持不變。
3. 誕生:如果當前單元格處於關閉狀態且計數正好為 3,則當前單元格開啟。
生命遊戲是一種全域細胞自動機,可以使用內建命令按如下方式實現CellularAutomaton,其中初始條件被指定為一個二進位制矩陣 ,並返回世代
到
的結果。(這裡,
對應於初始模式。)
Life[m_List?MatrixQ, {g1_Integer, g2_Integer}] :=
CellularAutomaton[
{
224,
{2, {{2, 2, 2}, {2, 1, 2}, {2, 2, 2}}},
{1, 1}
},
{m, 0},
g2,
{
{g1, g2},
Automatic
}] /; g2>=g1
從一代到下一代不發生變化的模式被稱為靜止生命,並被稱為具有周期 1。上面說明了幾個靜止生命。對於 個單元格,
, 2, 3, ... 的靜止生命的數量為 0, 0, 0, 2, 1, 5, 4, 9, 10, 25, 46, 121, 240, 619, 1353, ... (OEIS A019473)。
在一組配置中迴圈的模式稱為振盪器。
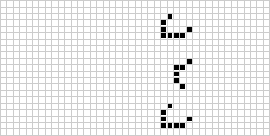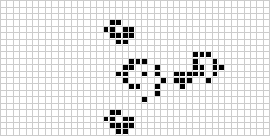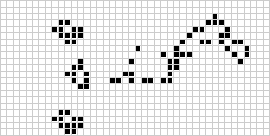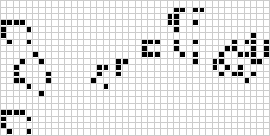
康威最初認為,沒有任何模式可以產生無限數量的單元格,並向任何能在 1970 年底之前找到反例的人提供了 50 美元的獎金(Gardner 1983,第 216 頁)。隨後發現了許多反例,包括槍和噴射列車(如上圖所示)。
沒有父模式的生命模式被稱為伊甸園(原因顯而易見)。第一個這樣的模式直到 1971 年才被發現,現在已知許多(LifeWiki)。

長期懸而未決的“唯一父問題”,即確定是否存在一種模式,該模式具有父模式但沒有祖父模式(Wainwright 1972,Gardner 1983,第 249 頁),由 Ilkka Törmä 和 Ville Salo 於 2022 年 1 月解決,他們發現了一個 374 個單元格的此類模式示例,這一結果很快被簡化為上面說明的 306 個單元格的模式(apgoucher 2022,LifeWiki)。
令人驚訝的是,生命是一種通用細胞自動機,從某種意義上說,它實際上能夠模擬任何細胞自動機、圖靈機或任何其他可以轉換為已知為通用的系統的系統。Berlekamp 等人 (1982) 和 Gosper (Gardner 1983, pp. 250-253) 獨立給出了生命通用性的證明概要。2000 年左右,P. Rendell (Rendell, Adamatzky 2001) 在生命中顯式實現了一個可以擴充套件為通用圖靈機的圖靈機。雖然 Rendell 的機器可以透過簡單地將其磁帶無限化而製成“真正的”通用計算機,但他既沒有注意到這一事實,也沒有提供通用圖靈機的實際構造。隨後,在 2002 年 11 月 11 日,P. Chapman 基於 D. Hickerson 的“滑動塊記憶體”方法構建了一種生命模式,該模式實現了通用暫存器機的操作。與 Rendell 圖靈機的有限磁帶不同,Chapman 機器的暫存器中的值是無界的,這使其成為生命遊戲中通用計算的真實模型。Chapman 的構造在 的區域中使用
個活動單元格,並且在 400 MHz 計算機上每秒可以計算大約 20 代。
更令人驚訝的是,正如 Wolfram (2002) 所表明的那樣,即使是一維細胞自動機(特別是規則 110)也可以是通用的。
已經構建了類似於生命但具有不同規則的二維細胞自動機遊戲,並命名為 HexLife 和 HighLife。HashLife 是一種生命演算法,它透過將子模式儲存在雜湊表中並使用它們向前跳過,有時一次跳過數千代,從而實現顯著的速度。