加法元胞自動機是一種元胞自動機,其規則與狀態的加法相容。通常,這種加法來源於模運算。加法規則允許獨立計算不同初始條件的演化,然後透過簡單相加來組合結果。因此,可以透過將單個細胞的演化與適當的卷積核(在雙色自動機的情況下,這將對應於初始“活動”細胞的集合)進行卷積,非常有效地計算任意起始條件的結果。
一個加法元胞自動機的簡單例子是由規則 90 基本元胞自動機提供的。從該規則的圖形表示可以看出,作為左鄰居、中心鄰居和右鄰居的函式,該規則僅僅由左鄰居和右鄰居的規則之和模 2 給出,其中白色細胞被賦值為 0,黑色細胞被賦值為 1。(這等同於 異或 運算,意味著“相加”兩個白色細胞或兩個黑色細胞得到一個白色細胞,而相加一個白色細胞和一個黑色細胞得到一個黑色細胞。)例如,規則 (1, 1, 1) 是 ,規則 (1, 1, 0) 是
,規則 (1, 0, 1) 是
,等等。對
種可能的鄰居狀態中的每一種重複此操作,得到
|
(1)
|
這正是定義規則 90 的二進位制字串(此規則被分配數字 90 是因為 在二進位制中)。

規則 90 的移位版本的演化如上圖所示。左圖顯示了規則 90 對由單個黑色方塊組成的初始條件進行的 31 次迭代。向右移動,每個圖都顯示了在起始條件中新增一個位移為 的額外黑色單元格的結果,每幀增加一代。

上面的圖示更明確地顯示了可加性。在這個動畫中,每一幀對應於初始條件,其中右側單元格進一步向右移動一個單位。可以看出,不重疊的模式部分保持不變,而重疊部分在異或運算下是可加的。
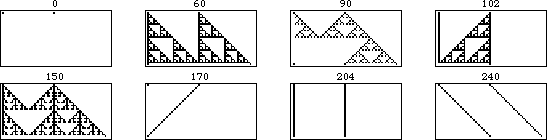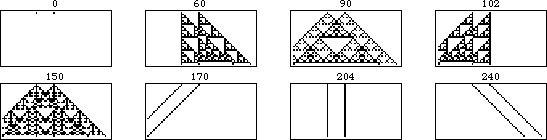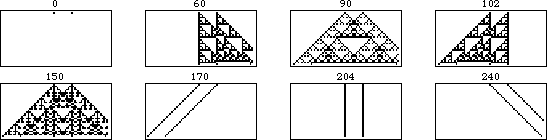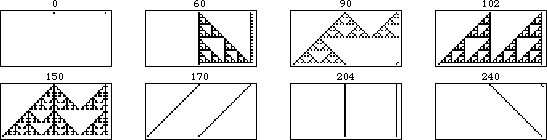
一般來說,具有 種顏色的元胞自動機是加法的,如果其規則可以寫成其鄰居的整數倍之和(模
),其中整數的範圍可以從 0 到
。因此,在
種可能的規則中,有
種加法規則,具有
種顏色和範圍
(Wolfram 2002, p. 952)。下表總結了基本元胞自動機的八個加法規則(
和
給出
)。在表中,
表示位於相對於中心位置
的鄰居。
對於上述自動機的可加性,所需的性質是結合律和交換律。可以將可加性的概念推廣到其他型別的加法。一般來說,設 表示
的元胞自動機演化歷史,設
表示作用於細胞值的二元運算子,並透過擴充套件作用於它們的狀態和演化。那麼,
是關於
的加法元胞自動機,如果
|
(2)
|
一些元胞自動機沒有有趣的 ,但另一些則有,並且這些加法可以用來加速計算。
規則 250 提供了在 或運算()下的加法基本元胞自動機的另一個例子。透過檢查規則集,可以驗證在每種情況下,如果任一(或兩者)鄰居是黑色的,則結果狀態為黑色,並且僅當兩個鄰居都是白色時才為白色。這對應於規則集
|
(3)
|
這與規則 250 的定義相同。


上面說明了前幾個移位的逐代差異以及作為移位函式的整個模式。
由於可加性,加法元胞自動機的演化行為類似於線性偏微分方程的解。特別是,它們允許格林函式的類似物,這樣,給定一個初始條件,可以透過將單個細胞的演化(可以看作是積分核的類似物)與初始條件進行卷積來找到結果演化(Wolfram 2002, p. 952)。