球面點拾取

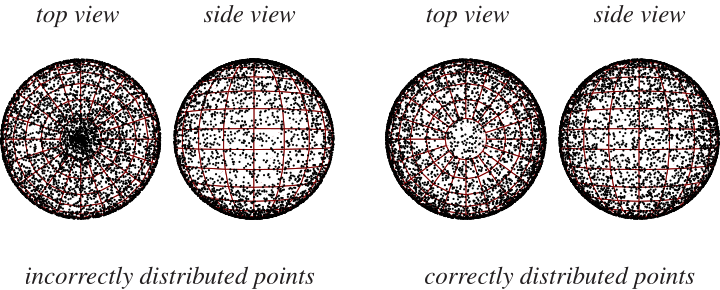
要在單位球面的表面上選取一個隨機點，選擇來自均勻分佈和的球面座標 和 是不正確的，因為面積元素 是 的函式，因此以這種方式選取的點將“聚集”在極點附近（如上左圖所示）。

可以使用 Wolfram 語言中的函式在單位球面上拾取 個隨機點：RandomPoint[Sphere[], n].

為了獲得這樣的點，使得球面上任何小區域預期包含相同數量的點（如上右圖所示），選擇 和 作為 上的隨機變數。然後

			(1)
			(2)

給出了均勻分佈在 上的點集的球面座標。這之所以有效，是因為立體角的微分元素由下式給出

(3)

極角的分佈 可以從下式找到

(4)

透過對 求 (2) 的導數得到 ，解 (2) 得到 ，並將結果代入 (4) 並令 ，得到分佈

(5)

類似地，我們可以選擇 均勻分佈（因此我們有 ），並獲得點

			(6)
			(7)
			(8)

其中 和 ，這些點也均勻分佈在 上。

Marsaglia (1972) 推匯出一個優雅的方法，該方法包括從 上的獨立均勻分佈中選取 和 ，並拒絕滿足 的點。從剩餘的點中，

			(9)
			(10)
			(11)

在單位球面的表面上具有均勻分佈。此方法也可以擴充套件到超球面點拾取。上面的圖顯示了 100、1000 和 5000 個初始點的分佈（其中計數指的是丟棄之前的點數）。

Cook (1957) 擴充套件了 von Neumann (1951) 的方法，給出了一個在單位球面的表面上均勻分佈地拾取點的簡單方法。從 上的均勻分佈中選取四個數字 、、 和 ，並拒絕滿足以下條件的點對

(12)

從剩餘的點中，四元數變換規則表明，具有笛卡爾座標的點

			(13)
			(14)
			(15)

具有所需的分佈 (Cook 1957, Marsaglia 1972)。上面的圖顯示了 100、1000 和 5000 個初始點的分佈（其中計數指的是丟棄之前的點數）。

拾取球面上隨機點的另一種簡單方法是生成三個高斯隨機變數 、 和 。然後，向量的分佈

(16)

在表面 上是均勻的 (Muller 1959, Marsaglia 1972)。