緊緻流形是作為拓撲空間是緊緻的流形。例子包括圓(唯一的一維緊緻流形)和維超球面和環面。二維緊緻流形完全由它們的定向和洞的數量(虧格)分類。應該注意的是,術語“緊緻流形”通常暗示“無邊界流形”,這是此處使用的意義。當需要一個單獨的術語時,緊緻無邊界流形被稱為閉流形。
對於拓撲學和幾何學中的許多問題,研究緊緻流形很方便,因為它們具有“良好”的行為。使緊緻流形“良好”的性質包括它們可以被有限多個座標圖覆蓋,並且任何連續實值函式在緊緻流形上都是有界的。
對於任何正整數,可以透過用莫比烏斯帶替換
個圓盤來產生不同的不可定向曲面。 特別地,用莫比烏斯帶替換一個圓盤會產生交叉曲面,而替換兩個圓盤會產生克萊因瓶。球面,
洞環面,以及這一系列的不可定向曲面構成了緊緻、無邊界二維流形的完整列表。
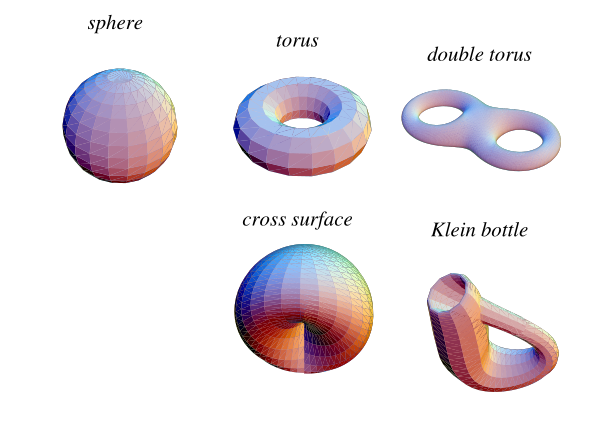
下表列出了小的二維緊緻流形的類別,這些類別也在上面進行了說明。