速度向量

速度向量的概念來自經典物理學。透過使用向量表示單個粒子的位置和運動，運動方程變得更簡單、更直觀。假設粒子在時間 的位置由位置向量 給出。那麼速度向量 是位置的導數，

例如，假設一個粒子被限制在平面上，其位置由 給出。那麼它以恆定速度沿著單位圓運動。其速度向量是 。在圖表中，將速度向量平移使其從 出發是有意義的。特別地，它被繪製為從 到 的箭頭。

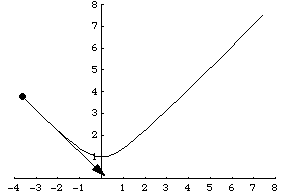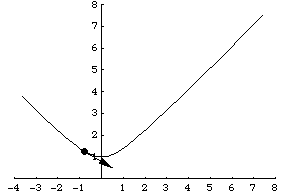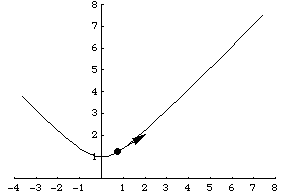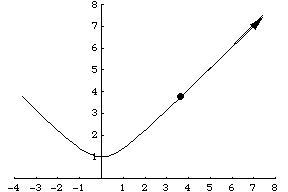
另一個例子是粒子沿著引數化表示為 的雙曲線運動。其速度向量然後由 給出，如上圖所示。

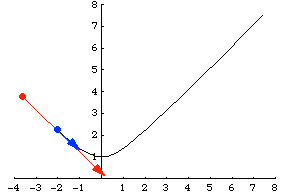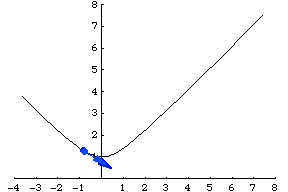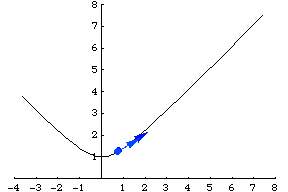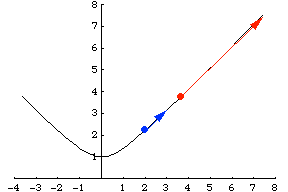
沿著相同的路徑行進，但使用不同的函式稱為重引數化，而鏈式法則描述了速度的變化。例如，雙曲線也可以透過 引數化。請注意，，並且根據鏈式法則，。

請注意，可能的速度向量的集合形成一個向量空間。如果 和 是透過原點的兩條路徑，那麼 也是，並且這條路徑的速度向量是 。類似地，如果 是一個標量，那麼路徑 的速度向量是 。區分不同點的速度向量是有意義的。在物理學中，所有速度向量的集合給出了位置和動量的所有可能組合，被稱為相空間。在數學中，速度向量形成切空間，而切空間的集合形成切叢。