五角二十四面體

製作你自己的五角二十四面體

列印並摺疊

3D 列印

五角二十四面體是扭稜立方體的 24 面對偶多面體。上面展示了它的線框版本和一個可用於其構造的網格。

礦物赤銅礦 () 以五角二十四面體晶體的形式形成 (Steinhaus 1999, pp. 207 and 209)。

它是 Wenninger 對偶 (W₁₇)。

因為它是一個手性扭稜立方體的對偶，所以五角二十四面體也以兩種對映異構形式出現，稱為左旋（左）和右旋（右）。上面展示了兩個對映體重疊在一起的吸引人的對偶。

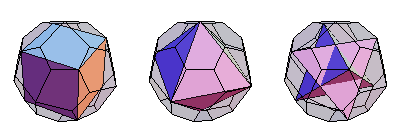
立方體、八面體和星形八面體都可以內接在五角二十四面體的頂點上 (E. Weisstein, Dec. 25, 2009)。

令人驚訝的是，三波那契常數 與五角二十四面體立方體的度量屬性密切相關。

其不規則五邊形面具有以下頂點角

			(1)
			(2)
			(3)

（四次）和

			(4)
			(5)
			(6)

（一次），其中 是一個多項式根， 是三波那契常數。

由單位邊長的扭稜立方體形成的對偶具有以下邊長

			(7)
			(8)
			(9)
			(10)
			(11)
			(12)

外接球半徑 由下式給出

			(13)
			(14)
			(15)

表面積 由下式給出

			(16)
			(17)
			(18)

和體積 由下式給出

			(19)
			(20)
			(21)