簡單圖的似然性定義為從集合 開始。然後迭代以下過程以產生階數為
的圖的集合
。在步驟
中,從集合
中隨機選擇一個整數
。現在隨機選擇
中的一個圖(保持其在步驟
中構建的機率),並從中新增一個新的頂點,該頂點連線到其現有頂點的
個隨機選擇的所有頂點。現在合併此過程產生的任何同構圖,方法是將其機率相加。則
在
個頂點上的圖的似然性定義為
出現在
中的機率。
此過程的第 次迭代產生
個節點上的每個可能的圖。上面說明了
到 4 個節點的圖的結果。E. Weisstein(2013 年 12 月 23 日)已經計算了最多 10 個節點的所有簡單圖的似然性。
,其中
是 圖的補圖
。
和
因此是同等可能的。
由於這些值是機率,因此所有 節點圖的似然性之和為 1,並且單個似然性滿足
|
(1)
|
其中 僅對
成立。
也滿足更強的不等式
 |
(2)
|
其中 是 圖的自同構群 的階數
(Banerji et al. 2014)。
下表總結了許多特殊類別的成員的似然性。
| 圖 | OEIS | 值 |
| Andrásfai 圖 | A000000/A000000 | |
| 反稜柱圖 | A000000/A000000 | 13/21600, 1909/2540160000, ... |
| 啞鈴圖 | A000000/A000000 | 97/129600, 79/282240000, ... |
| 雞尾酒會圖 | A000000/A000000 | 1/2, 1/36, 13/21600, 11/1587600, ... |
| 完全圖 | A000000/A000000 | 1, 1/2, 1/6, 1/24, 1/120, 1/720, ... |
| 冠圖 | A000000/A000000 | 29/64800, 11/40642560, ... |
| 迴圈圖 | A000000/A000000 | 1/2, 1/270, 1909/2540160000, ... |
| 空圖 | A000000/A000000 | 1, 1/2, 1/6, 1/24, 1/120, 1/720, ... |
| 超立方體圖 | A000000/A000000 | 1, 1/2, 1/36, 11/40642560, ... |
| 梯形圖 | A000000/A000000 | 1/2, 1/36, 61/43200, 20299/2540160000, ... |
| 梯子橫檔圖 | A000000/A000000 | 1/2, 1/36, 13/21600, 11/1587600, ... |
| 莫比烏斯梯子 | A000000/A000000 | 23/259200, 1909/2540160000, ... |
| 路徑圖 | A000000/A000000 | 1, 1/2, 1/3, 1/9, 29/1080, 2/405, 2509/3402000, 1889/20412000, ... |
| 稜柱圖 | A000000/A000000 | 29/64800, 11/40642560, ... |
| 星圖 | A000000/A000000 | 1, 1/2, 1/3, 5/72, 17/1440, 77/43200, 437/1814400 |
| 太陽圖 | A000000/A000000 | 59/25920, 101/9072000, ... |
| 三角圖 | A000000/A000000 | 1, 1/6, 13/21600, ... |
| 輪圖 | A000000/A000000 | 1/24, 13/720, 203/129600, 2393/18144000, ... |
具有已知閉式值的類別包括
|
(3)
| |||
|
(4)
| |||
 |
(5)
| ||
|
(6)
| |||
 |
(7)
|
其中 是一個 完全圖,
是一個 空圖,
是一個 星圖,
是一個 梯子橫檔圖,
是一個 階乘,並且
是一個 次階乘。此外,迴圈圖 的
和 路徑圖 的
之間存在關係,由下式給出
|
(8)
|
(Banerji et al. 2014)。
一般來說,具有 個頂點和
個孤立邊的圖的似然性為
 |
(9)
| ||
 |
(10)
|
給出特殊情況
|
(11)
| |||
|
(12)
|
其中 是一個 調和數。
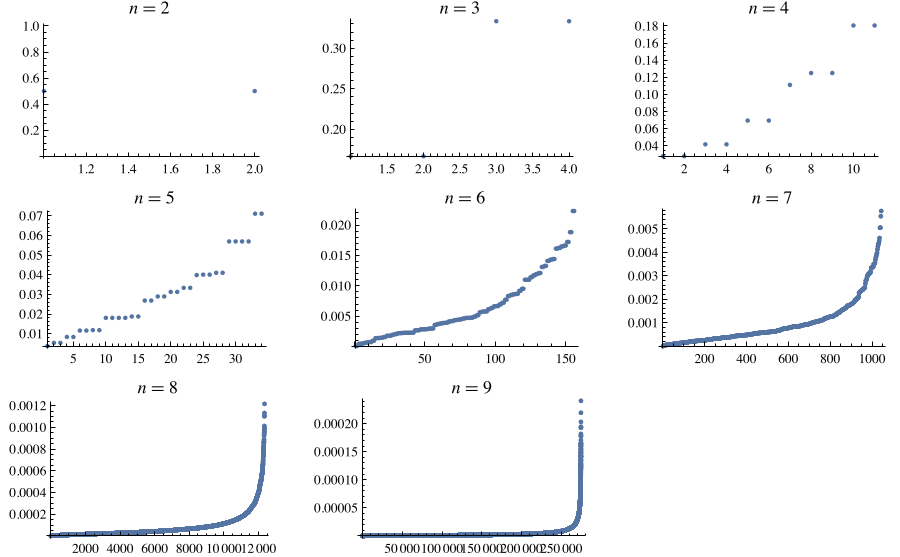
上面繪製了 對於
節點圖的值。
對於 的所有值,除了
、3 和 5(對於它們,最小值分別出現在
、
和
時),
的最小值出現在 完全二部圖
及其 圖的補圖。對於
,
, 2, ... 的最小值分別為 1, 1/2, 1/6, 1/36, 1/270, 23/259200, 319/54432000, 319/15240960000, ... (OEIS A234234 和 A234235)。
最大值 作為
的函式的情況不太清楚,對於
, 2, ...,最大值出現在
、
、
、爪形圖、鏢形圖、... 及其補圖。相應的最大值是 1, 1/2, 1/3, 13/72, 307/4320, 1927/86400, 39211/6804000, 27797639/22861440000, ... (OEIS A234236 和 A234237)。