高斯整數

高斯整數是 複數 ，其中 和 是 整數。高斯整數是 虛二次域 的成員，並構成一個通常表示為 的環，有時也表示為 （Hardy 和 Wright 1979，第 179 頁）。兩個高斯整數的和、差和積是高斯整數，但 僅當存在 使得

(1)

(Shanks 1993)。

高斯整數可以根據其他高斯整數（稱為高斯素數）唯一分解，直到 冪 和重排。

的單位是 和 。

高斯整數範數的一個定義是其復模量

(2)

另一個常見的定義（例如，Herstein 1975；Hardy 和 Wright 1979，第 182 頁；Artin 1991；Dummit 和 Foote 2004）將高斯整數的範數定義為

(3)

上述量的平方。（請注意，高斯整數形成一個 歐幾里得環，這正是使它們特別受關注的原因，僅在後一種定義下成立。）由於存在兩種可能的定義，因此在查閱文獻時需要謹慎。

兩個高斯整數 和 互素的機率是

(4)

(OEIS A088454)，其中 是 卡塔蘭常數 (Pegg; Collins and Johnson 1989; Finch 2003, p. 601)。

每個高斯整數都在高斯整數 的倍數的 範圍內。

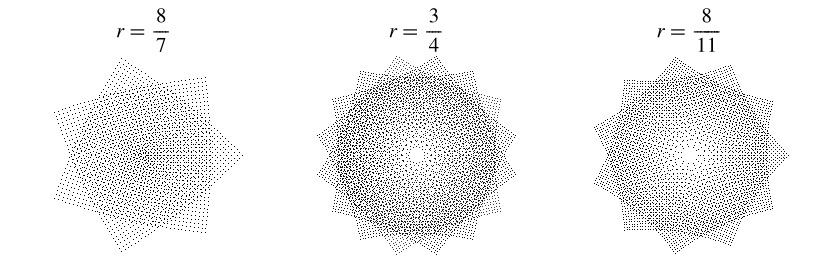
上面的圖顯示了高斯整數 對於各種有理值 的根（Trott 2004，第 24 頁）。