
|
|
|
螺線截面是一環面與垂直於環面中平面且垂直於平面 的平面的交線的曲線方程。(環面與平面的通常交線稱為環面截線)。設環面的管子半徑為
,其中平面位於
平面內,並且管子的中心距離原點
。現在用平面
切割環面。具有
的環面方程給出以下方程
|
(1)
|
|
(2)
|
|
(3)
|
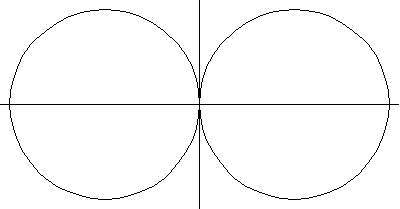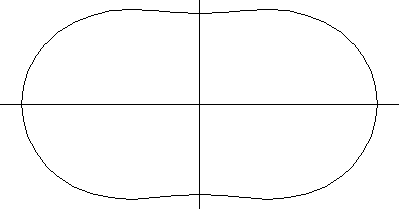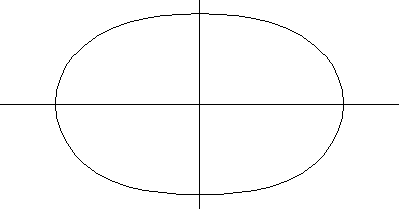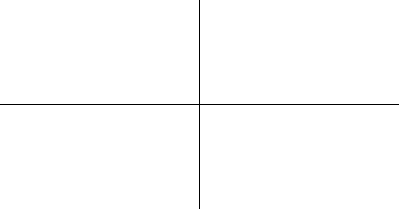
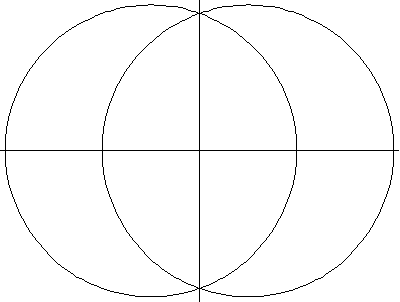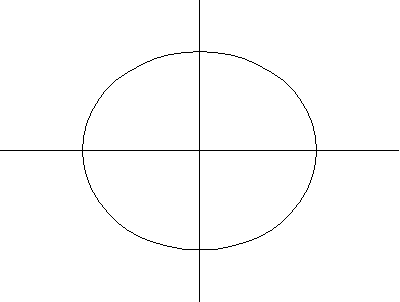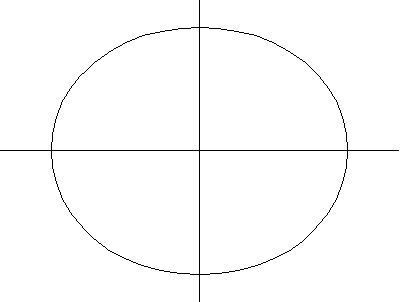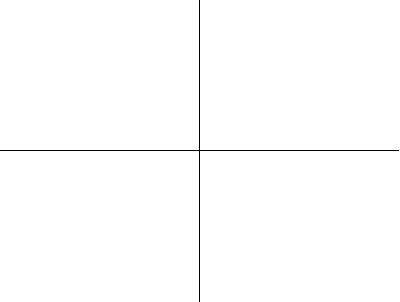
以上繪圖分別顯示了圓環環面、角環面和紡錘環面的一系列螺線截面。當 時,曲線由兩個圓組成,半徑為
,其中心位於
和
。如果
,則曲線由一個點(原點)組成;而如果
,則曲線上沒有點。
螺線擴充套件是圓錐曲線的擴充套件,由梅內克繆斯(Menaechmus)在公元前 150 年左右透過用平面切割圓錐而構建,並由希臘數學家珀爾修斯(Perseus)在公元 50 年左右首次考慮(MacTutor)。
如果 ,則 (3) 簡化為
|
(4)
|
這是卡西尼卵形線的方程。卡西尼卵形線因此是螺線截面。此外,以這些曲線作為橫截面的表面是上面所示的卡西尼曲面,修改之處在於垂直分量是平方而不是四次方。