韋爾群

設 為有限維分裂 半單李代數，定義在特徵為 0 的 域 上， 為分裂 卡 Cartan 子代數，且 為 在 的表示中的權。則

也是一個權。此外，反射 ，其中 是根，生成 中的線性變換群，稱為 相對於 的韋爾群 ，其中 是 的 代數共軛空間，而 是由根張成的 Q-空間 (Jacobson 1979, pp. 112, 117, and 119)。

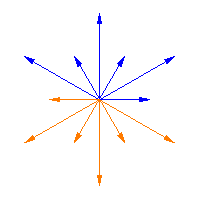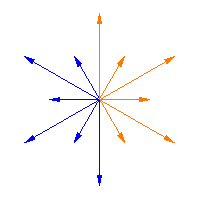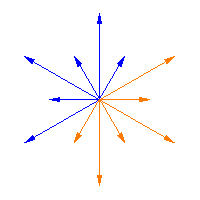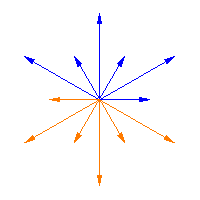
韋爾群作用於半單李代數的根，它是一個有限群。上面的動畫展示了韋爾群作用於從一個韋爾矩陣到下一個韋爾矩陣的同倫的根上的這種作用（即，它將箭頭從 滑動到 ），在前兩個圖中，而第三個圖顯示了韋爾群作用於半單李代數 的無限族的 Cartan 矩陣 的根（參見 Dynkin 圖），這是 特殊線性李代數 。