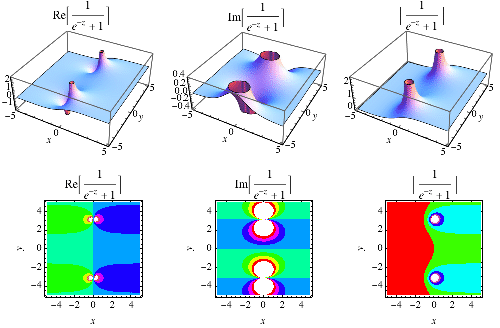
 |
Sigmoid 函式,也稱為 Sigmoid 曲線 (von Seggern 2007, p. 148) 或 Logistic 函式,是以下函式
|
(1)
|
它的導數為
|
(2)
| |||
|
(3)
| |||
|
(4)
|
和 不定積分
|
(5)
| |||
|
(6)
|
它具有 麥克勞林級數
|
(7)
| |||
 |
(8)
| ||
|
(9)
|
它在 處有一個拐點,其中
|
(10)
|
它也是 常微分方程
|
(11)
|
以及初始條件 的解。
 |
Sigmoid 函式,也稱為 Sigmoid 曲線 (von Seggern 2007, p. 148) 或 Logistic 函式,是以下函式
|
(1)
|
它的導數為
|
(2)
| |||
|
(3)
| |||
|
(4)
|
和 不定積分
|
(5)
| |||
|
(6)
|
它具有 麥克勞林級數
|
(7)
| |||
 |
(8)
| ||
|
(9)
|
它在 處有一個拐點,其中
|
(10)
|
它也是 常微分方程
|
(11)
|
以及初始條件 的解。
Weisstein, Eric W. "Sigmoid 函式。" 來自 --一個 資源。 https://mathworld.tw/SigmoidFunction.html