心形曲線

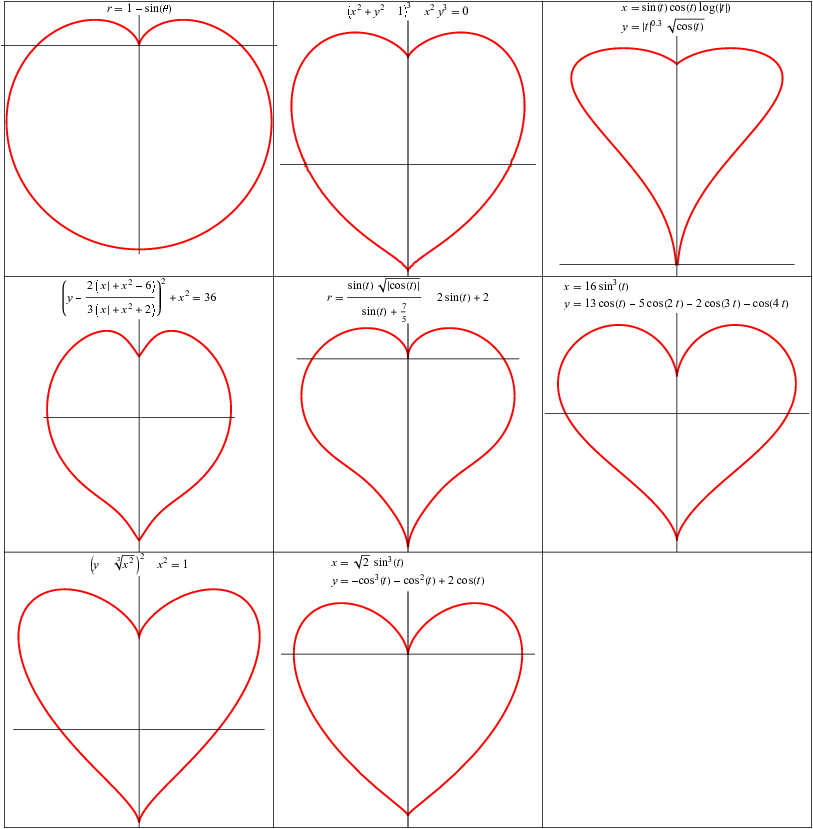
有許多數學曲線可以產生心形，上面展示了一些。 “第零”曲線是一個旋轉的心臟線（其名稱意為“心形”），由極座標方程給出

第一個心形曲線是透過取橫截面並將座標重新標記為得到的，從而得到 6 階代數方程

第二個心形曲線由引數方程給出

其中 (H. Dascanio, 私人通訊, 2003年6月21日)。

第三個心形曲線由下式給出

(P. Kuriscak, 私人通訊, 2006年2月12日)。這個心形曲線的每一半都是 6 階代數曲線的一部分。

第四個曲線是極座標曲線

來自匿名來源，並於 2010 年 2 月初從 的日誌檔案中獲得。這個心形曲線的每一半都是 12 階代數曲線的一部分，因此整個曲線是 24 階代數曲線的一部分。

第五個心形曲線可以引數化定義為

第六個心形曲線由簡單的表示式給出

(由 J. Schroeder 在賀卡上註明，私人通訊，2021年10月16日)。當使用比例引數和正確無量綱化後，曲線變為

這可以寫成關於和的六次方程。

第七個心形曲線可以引數化定義為

這是透過修改腎臟線的引數方程而產生的 (J. Mangaldan, 私人通訊, 2023年2月14日)。

這些心形的面積是

其中可以以閉合形式給出，作為超幾何函式、反三角函式和伽瑪函式的複雜組合。

Bonne 投影是一種地圖投影，它將球體的表面對映到如上所示的心形區域。