主題
Search

卷積

DOWNLOAD Mathematica Notebook下載 Wolfram Notebook

卷積是一個積分，表示一個函式 g 在另一個函式 f 上滑動時，它們之間的重疊量。因此，它將一個函式與另一個函式“混合”。例如，在合成成像中，測量的髒圖是“真實” CLEAN 圖與髒束（取樣分佈的 傅立葉變換）的卷積。卷積有時也以其德語名稱 faltung（“摺疊”）而聞名。

卷積在 Wolfram 語言 中實現為Convolve[f, g, x, y] 和DiscreteConvolve[f, g, n, m]。

抽象地說，卷積定義為函式 f 和 g 的乘積，它們是 R^n 中 Schwartz 函式代數中的物件。兩個函式 f 和 g 在有限範圍 [0,t] 上的卷積由下式給出

[f*g](t)=int_0^tf(tau)g(t-tau)dtau,
(1)

其中符號 [f*g](t) 表示 f 和 g 的卷積。

卷積更常在無限範圍內進行，

f*g=int_(-infty)^inftyf(tau)g(t-tau)dtau
(2)
=int_(-infty)^inftyg(tau)f(t-tau)dtau
(3)

(Bracewell 1965, p. 25) 變數（在本例中為 t）是隱含的，有時也寫成 f tensor g。

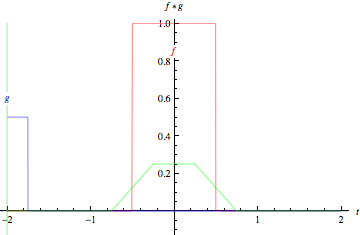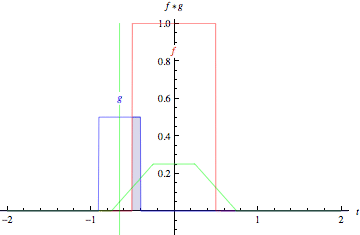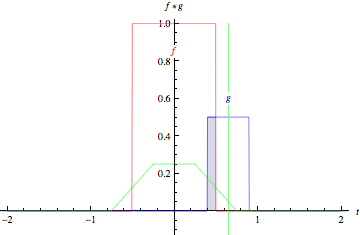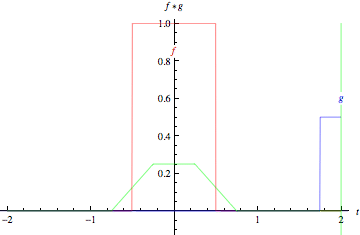
Convolution of two rectangle functions
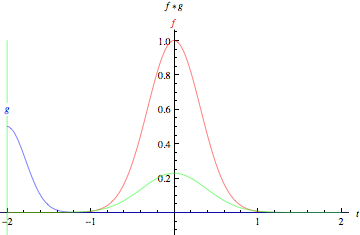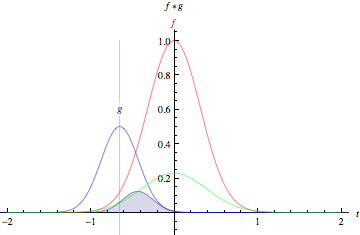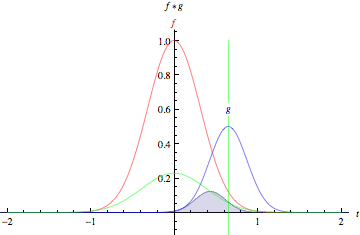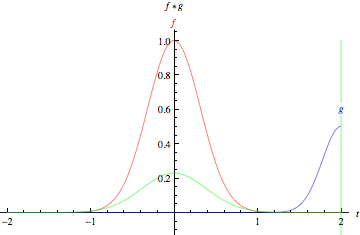
Convolution of two Gaussian functions

上面的動畫以圖形方式說明了兩個 矩形函式（左）和兩個 高斯函式（右）的卷積。在圖中，綠線顯示了藍色和紅色曲線的卷積，作為 t 的函式，位置由垂直綠線指示。灰色區域表示乘積 g(tau)f(t-tau) 作為 t 的函式，因此其面積作為 t 的函式正是卷積。需要強調的一個特徵，並且這些圖示沒有表達出來（因為它們都專門涉及對稱函式）是函式 g 必須在將其在 f 上滯後並積分之前進行映象。

兩個 矩形函式 f=Pi_(t_1,t_2)(t) 和 g=Pi_(u_1,u_2)(t) 的卷積具有特別簡單的形式

f*g=[(t-t_1-u_1)H(t-t_1-u_1)-(t-t_2-u_1)H(t-t_2-u_1) -(t-t_1-u_2)H(t-t_1-u_2)+(t-t_2-u_2)H(t-t_2-u_2)],
(4)

其中 H(x) 是 Heaviside 階躍函式。更令人驚訝的是，兩個高斯函式的卷積

f=e^(-(t-mu_1)^2/(2sigma_1^2))/(sigma_1sqrt(2pi))
(5)
g=e^(-(t-mu_2)^2/(2sigma_2^2))/(sigma_2sqrt(2pi))
(6)

是另一個高斯函式

f*g=1/(sqrt(2pi(sigma_1^2+sigma_2^2)))e^(-[t-(mu_1+mu_2)]^2/[2(sigma_1^2+sigma_2^2)]).
(7)

設 f、g 和 h 為任意函式，a 為常數。卷積滿足以下性質

f*g=g*f
(8)
f*(g*h)=(f*g)*h
(9)
f*(g+h)=(f*g)+(f*h)
(10)

(Bracewell 1965, p. 27)，以及

a(f*g)=(af)*g
(11)
=f*(ag)
(12)

(Bracewell 1965, p. 49)。

對卷積求導得到

(f*g)^'=f^'*g
(13)
=f*g^'
(14)

(Bracewell 1965, p. 119)。

卷積下的面積是因子下方面積的乘積，

int_(-infty)^infty(f*g)dt=int_(-infty)^infty[int_(-infty)^inftyf(u)g(t-u)du]dt
(15)
=int_(-infty)^inftyf(u)[int_(-infty)^inftyg(t-u)dt]du
(16)
=[int_(-infty)^inftyf(u)du][int_(-infty)^inftyg(t)dt].
(17)

卷積的水平函式質心相加

<t>_(f*g)=<t>_f+<t>_g,
(18)

並且如果 f 或 g 的函式質心位於其原點，則方差也一樣

<t^2>_(f*g)=<t^2>_f+<t^2>_g
(19)

(Bracewell 1965, p. 142)，其中

<t^n>_f=(int_(-infty)^inftyt^nf(t)dt)/(int_(-infty)^inftyf(t)dt).
(20)

在機率論中，卷積還有另一個定義，由下式給出

F(t)*G(t)=intF(t-x)dG(x),
(21)

其中 intF(t-x)dG(x) 是 Stieltjes 積分。

另請參閱

自相關, 柯西乘積, 卷積定理, 互相關, 迴圈圖, 維納-辛欽定理 在 課堂中探索這個主題

使用 探索

參考文獻

Bracewell, R. "Convolution" and "Two-Dimensional Convolution." Ch. 3 in The Fourier Transform and Its Applications. New York: McGraw-Hill, pp. 25-50 and 243-244, 1965.Hirschman, I. I. and Widder, D. V. The Convolution Transform. Princeton, NJ: Princeton University Press, 1955.Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 464-465, 1953.Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Convolution and Deconvolution Using the FFT." §13.1 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 531-537, 1992.Weisstein, E. W. "Books about Convolution." http://www.ericweisstein.com/encyclopedias/books/Convolution.html.

在 中引用

卷積

請引用為

Weisstein, Eric W. “卷積。” 來自 —— 資源。 https://mathworld.tw/Convolution.html

主題分類