C^infty 函式

一個 函式是指對於所有階數求導都可微的函式。例如， (上圖左側) 是 函式，因為它的第 階導數 存在且連續。所有多項式都是 函式。使用這種符號的原因是 C-k 函式具有 階連續導數。

函式也稱為“光滑”函式，因為它們及其導數都沒有“角”，否則會使它們的圖形看起來有些粗糙。例如， 不是光滑的（上圖右側）。

存在一些特殊的 函式，它們在分析和幾何學中非常有用。例如，存在稱為隆起函式的光滑函式，它們是特徵函式的光滑近似。通常，這些函式需要一些微積分來證明它們確實是 函式。

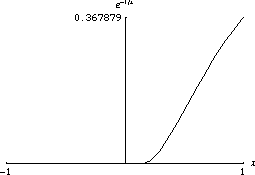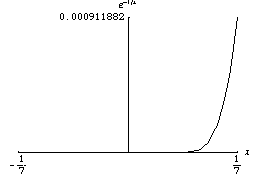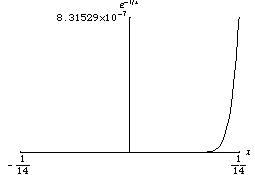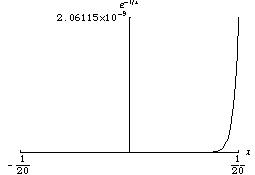
任何解析函式都是光滑的。但是光滑函式不一定是解析函式。例如，解析函式不能是隆起函式。考慮以下函式，它在 0 處的泰勒級數恆等於零，但該函式不為零

(1)

函式 非常迅速地趨於零。光滑函式的一個性質是它們在不同尺度下可能看起來非常不同。

光滑函式的集合不能構成巴拿赫空間，這使得一些問題變得困難，但它具有較弱的弗雷歇空間結構。