C^k 函式

具有 個連續 導數的函式稱為 函式。為了指定在域 上的 函式，使用符號 。最常見的 空間是 ，即 連續函式的空間，而 是 連續可微函式的空間。 Cartan (1977, p. 327) 幽默地寫道：“透過‘可微’，我們指的是 C^k 類，其中 儘可能大。”

當然，任何光滑函式都是 函式，並且當 時，任何 函式都是 函式。很自然地認為 函式有點粗糙，但 函式的圖形“看起來”很光滑。

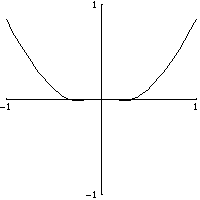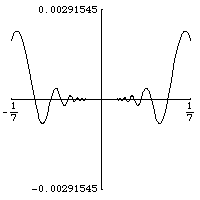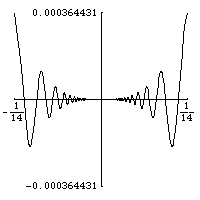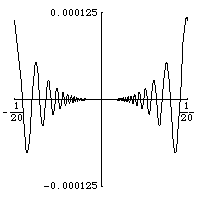
函式的例子有 （當 為偶數時）和 ，它們在 0 處沒有第 階導數。

函式的概念可以被限制為那些前 階導數是有界函式的函式。這種限制的原因是 函式的集合有一個範數，使其成為巴拿赫空間，