譜序列是同調代數中的一個工具,在代數、代數幾何和代數拓撲中有著廣泛的應用。 粗略地說,譜序列是一個用於跟蹤具有相互對映的正合序列集合的系統。
譜序列有很多定義,並且存在許多細微的變體,這些變體在某些特定目的中非常有用。 最常見的型別是“第一象限上同調譜序列”,它是一系列阿貝爾群 ,其中
、
和
是整數,其中
和
為非負整數,且
對於某個正整數
,通常為 2。 群
配備有對映
|
(1)
|
使得
|
(2)
|
還有進一步的限制,即
|
(3)
|
對映 被稱為邊界對映。
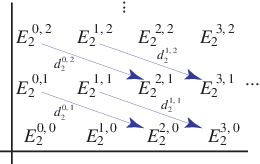
譜序列可以被視覺化為一系列網格,每個網格對應一個 值。
和
表示網格上的位置,其中
是
座標,
是
座標。 上圖顯示了
的情況。
群 的整個集合及其邊界對映被稱為
-項。 群
完全由
-項確定
對於給定的 和
值,群
最終會穩定下來,因為只有有限數量的非零邊界對映以該位置開始或結束。 這個穩定值被稱為
。 穩定值允許定義譜序列的收斂性。 特別是,譜序列
收斂到群
,寫作
|
(4)
|
如果存在一個濾子
|
(5)
|
使得連續商等於 項,即,
|
(6)
|
|
(7)
|
是一個纖維化(例如,Hopf 對映 )。 那麼存在一個譜序列,其
-項為
|
(8)
|
該序列收斂到 。(這裡,
表示普通上同調,與上面的
無關。) 這允許人們從其他兩個空間的上同調計算三個空間
、
和
之一的上同調。
還有其他譜序列的例子。 Leray-Serre 譜序列用於計算層復形的超上同調。 Grothendieck 譜序列用於從兩個原始函子的匯出函子計算兩個函子組合的匯出函子。 Leray-Serre 譜序列是 Grothendieck 譜序列的一個特例。 最後,Adams 譜序列用於計算球體的高階同倫群。