主題
Search

Pochhammer 符號

DOWNLOAD Mathematica Notebook下載 Wolfram Notebook
PochhammerSymbol

Pochhammer 符號

(x)_n=(Gamma(x+n))/(Gamma(x))
(1)
=x(x+1)...(x+n-1)
(2)

(Abramowitz 和 Stegun 1972, p. 256; Spanier 1987; Koepf 1998, p. 5) 對於 n>=0 是一種不幸的記號，在特殊函數理論中用於 上升階乘，也稱為上升階乘冪 (Graham et al. 1994, p. 48) 或上升階乘 (Boros 和 Moll 2004, p. 16)。Pochhammer 符號在 Wolfram 語言 中實現為Pochhammer[x, n].

在組合數學中，記號 x^((n)) (Roman 1984, p. 5)、<x>_n (Comtet 1974, p. 6) 或 x^(n^_) (Graham et al. 1994, p. 48) 用於 上升階乘，而 (x)_n 或 x^(n__) 表示 下降階乘 (Graham et al. 1994, p. 48)。因此，在解釋記號 (x)_n 和 x^((n)) 時需要格外小心。

(x)_n 對於非負整數 n 的前幾個值為

(x)_0=1
(3)
(x)_1=x
(4)
(x)_2=x^2+x
(5)
(x)_3=x^3+3x^2+2x
(6)
(x)_4=x^4+6x^3+11x^2+6x
(7)

(OEIS A054654)。

以閉合形式，(x)_n 可以寫成

(x)_n=sum_(k=0)^n(-1)^(n-k)s(n,k)x^k,
(8)

其中 s(n,k) 是 第一類斯特林數。

Pochhammer 符號滿足

(-x)_n=(-1)^n(x-n+1)_n,
(9)

二等分公式

(x)_(2n)=2^(2n)(x/2)_n((1+x)/2)_n
(10)
(x)_(2n+1)=2^(2n+1)(x/2)_(n+1)((1+x)/2)_n,
(11)

和倍增公式

(2x)_n={2^n(x)_(n/2)(x+1/2)_(n/2) for n even; 2^n(x)_((n+1)/2)(x+1/2)_((n-1)/2) for n odd
(12)

(Boros 和 Moll 2004, p. 17)。

Pochhammer 符號的比率以閉合形式給出為

((x)_n)/((x)_m)={(x+m)_(n-m) if n>=m; 1/((x+n)_(m-n)) if n<=m
(13)

(Boros 和 Moll 2004, p. 17)。

導數由下式給出

d/(dx)(x)_n=(x)_n[psi_0(n+x)-psi_0(x)],
(14)

其中 psi_0(x) 是 雙伽瑪函式。

特殊值包括

(1)_n=n!
(15)
(1/2)_n=((2n-1)!!)/(2^n).
(16)

Pochhammer 符號 (x)_n 服從尤拉的變換

sum_(n=0)^infty((a)_n)/(n!)a_nz^n=(1-z)^(-a)sum_(n=0)^infty((a)_n)/(n!)Delta^na_0(z/(1-z))^n,
(17)

其中 Delta 是 前向差分，並且

Delta^ka_0=sum_(m=0)^k(-1)^m(k; m)a_(k-m)
(18)

(Nørlund 1955)。

1/(k)_p 的和可以以閉合形式完成，如下所示

sum_(k=1)^n1/((k)_p)=1/((p-1)Gamma(p))-(nGamma(n))/((p-1)Gamma(n+p))
(19)

對於 p>1。

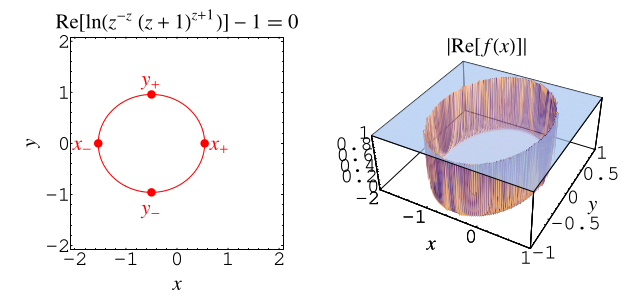
PochhammerProductCurve

考慮乘積

f(z)=lim_(k->infty)product_(i=0)^(k)(z+i/k)
(20)
=lim_(k->infty)(1/k)^(k+1)(kz)_(k+1).
(21)

此函式收斂到 0、有限值或發散，具體取決於 z 的值。臨界曲線由 隱式方程 給出

R[-1+ln(z^(-z)(1+z)^(1+z))]=0.
(22)

在此曲線內部，函式收斂到 0，而在其外部，函式發散。發生收斂的最大實數值由 x_+=0.54221... (OEIS A090462) 給出，最小值由 x_-=-(1+x_+) 給出。y 的極值由 y_+/-=+/-0.95883... (OEIS A090463) 給出。在臨界輪廓上，f(z) 取值為

f(z)=1/2[lnz+ln(z+1)].
(23)
PochhammerProductSurface

繪製適當縮放版本的 f(z)，其中 k 是有限的，顯示出美麗而微妙的結構，例如上面為 k=100 所示的結構 (M. Trott，私人通訊，2003 年 12 月 1 日)。

PochhammerProductSinArg

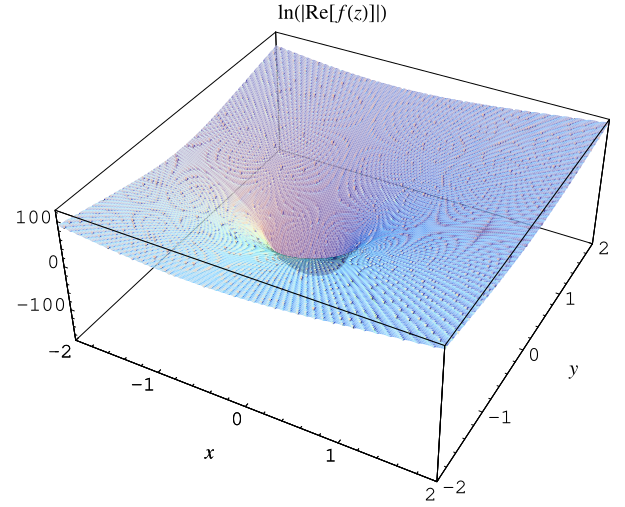
另一個精美的視覺化圖繪製了 sin(arg(f(z)))，如上面為 k=2048 所示 (M. Trott，私人通訊，2003 年 12 月 2 日)。

另請參閱

階乘, 下降階乘, 廣義超幾何函式, Hankel 符號, 調和對數, 超幾何函式, Kramp 符號, 上升階乘

相關的 Wolfram 網站

http://functions.wolfram.com/GammaBetaErf/Pochhammer/

使用 探索

參考文獻

Abramowitz, M. 和 Stegun, I. A. (編). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, 1972.Boros, G. 和 Moll, V. Irresistible Integrals: Symbolics, Analysis and Experiments in the Evaluation of Integrals. Cambridge, England: Cambridge University Press, 2004.Comtet, L. Advanced Combinatorics: The Art of Finite and Infinite Expansions, 修訂增補版. Dordrecht, Netherlands: Reidel, 1974.Erdélyi, A.; Magnus, W.; Oberhettinger, F.; 和 Tricomi, F. G. Higher Transcendental Functions, Vol. 1. New York: Krieger, p. 52, 1981.Graham, R. L.; Knuth, D. E.; 和 Patashnik, O. Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley, 1994.Koepf, W. Hypergeometric Summation: An Algorithmic Approach to Summation and Special Function Identities. Braunschweig, Germany: Vieweg, 1998.Nørlund, N. E. "Hypergeometric Functions." Acta Math. 94, 289-349, 1955.Roman, S. The Umbral Calculus. New York: Academic Press, p. 5, 1984.Sloane, N. J. A. Sequences A054654, A090462, and A090463 in "The On-Line Encyclopedia of Integer Sequences."Spanier, J. 和 Oldham, K. B. "The Pochhammer Polynomials (x)_n." 第 18 章，載於 An Atlas of Functions. Washington, DC: Hemisphere, pp. 149-165, 1987.

在 中被引用

Pochhammer 符號

請引用為

Weisstein, Eric W. "Pochhammer 符號。" 來自 Web 資源。 https://mathworld.tw/PochhammerSymbol.html

主題分類