透過三角形質心 的給定三角形
和第二 Brocard 三角形的頂點對的三個外接圓被稱為 McCay 圓(Johnson 1929, p. 306)。
它們的圓心(即第二 Brocard 三角形的圓心)的外接圓因此是Brocard 圓。
-McCay 圓的圓心函式為
和半徑,
是 Neuberg 圓 的 1/3,其中 是 Brocard 角 (Johnson 1929, p. 307)。
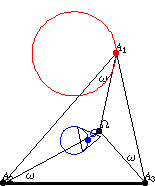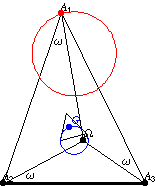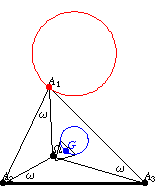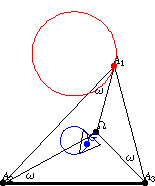
如果 多邊形頂點 的 三角形 描述一個 Neuberg 圓
,那麼它的三角形質心
描述其中一個 McCay 圓(Johnson 1929, p. 290)。在上圖中,內三角形是
的第二 Brocard 三角形,其兩個指示的邊與
共圓在 McCay 圓上。