紐伯格圓

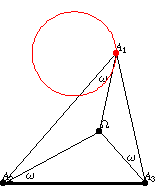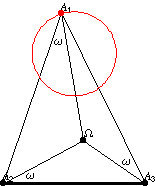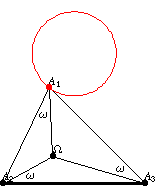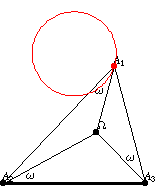
紐伯格 -圓是在給定底邊 和給定布羅卡角 的三角形中，多邊形頂點 的軌跡。從中心 ，底邊 對向角 。對於三角形的另外兩條邊，可以重複相同的步驟，總共得到三個紐伯格圓。類似地，透過主圓在三角形各自邊上的反射，可以獲得中心為 , , 和 的三個反射紐伯格圓。

A-圓的方程可以透過將底邊設為 (0, 0), (, 0) 並解以下方程求得

			(1)
			(2)

同時使用以下公式消除 和

(3)

其中 是三角形 的面積。解 x 得

(4)

平方並完成平方後得到

(5)

因此，這條邊上的紐伯格圓 的圓心為

(6)

半徑為

(7)

紐伯格圓的圓心稱為紐伯格中心，由紐伯格中心確定的三角形稱為第一和第二紐伯格三角形。

沒有任何 Kimberling 中心位於任何紐伯格圓或紐伯格反射圓上。

紐伯格圓的圓引數由下式給出

			(8)
			(9)
			(10)

第一紐伯格三角形 （左圖）和反射第一紐伯格三角形 （右圖）如上圖所示。

在給定直線的一側作為底邊，可以構造六個與給定不等邊三角形直接或間接相似的三角形，並且這些三角形的頂點位於它們的公共紐伯格圓上（Johnson 1929，p. 289）。