有三個與垂足圓相關的定理,統稱為 Fontené 定理。
第一個 Fontené 定理是,設 為一個三角形,
為任意點,
為
的中點三角形,
為
關於
的垂足三角形。 將
和
的對應邊的交點表示為
,
, 和
(例如,
是
和
的交點,等等),那麼直線
,
和
交於一點
,該點
也位於
(即
的九點圓) 和
(即
關於
的垂足圓) 的外接圓上。
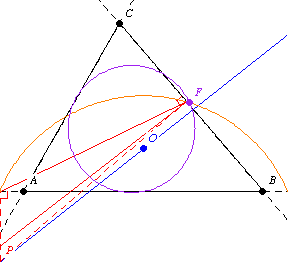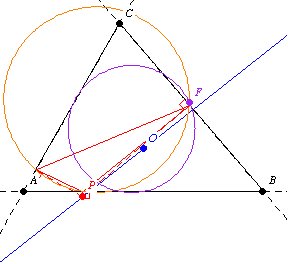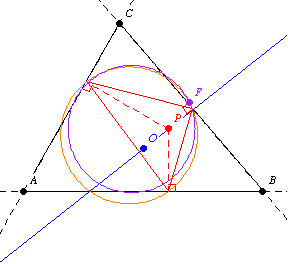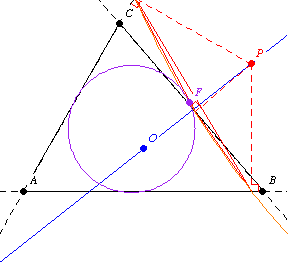
第二個 Fontené 定理指出,如果一個點在一個透過外心的固定線上移動,那麼它的垂足圓會透過九點圓上的一個固定點,如上圖所示。
第三個 Fontené 定理指出,點 的垂足圓與九點圓相切,當且僅當
及其等角共軛點
位於透過外心的直線上。(請注意,Johnson (1929) 錯誤地陳述了這個定理,用垂心代替了外心。)Feuerbach 定理是這個定理的一個特例。