另請參閱
分支,
餘維數,
費根鮑姆常數,
費根鮑姆函式,
翻轉分岔,
摺疊分岔,
Hopf 分岔,
邏輯斯蒂對映,
週期倍增,
叉形分岔,
跨臨界分岔
使用 探索
參考文獻
Guckenheimer, J. and Holmes, P. "Local Bifurcations." Ch. 3 in Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields, 2nd pr., rev. corr. New York: Springer-Verlag, pp. 117-165, 1983.Lichtenberg, A. J. and Lieberman, M. A. "Bifurcation Phenomena and Transition to Chaos in Dissipative Systems." Ch. 7 in Regular and Chaotic Dynamics, 2nd ed. New York: Springer-Verlag, pp. 457-569, 1992.Rasband, S. N. "Asymptotic Sets and Bifurcations." §2.4 in Chaotic Dynamics of Nonlinear Systems. New York: Wiley, pp. 25-31, 1990.Weisstein, E. W. "Books about Chaos." http://www.ericweisstein.com/encyclopedias/books/Chaos.html.Wiggins, S. "Local Bifurcations." Ch. 3 in Introduction to Applied Nonlinear Dynamical Systems and Chaos. New York: Springer-Verlag, pp. 253-419, 1990.在 中被引用
分岔
引用為
Weisstein, Eric W. “分岔。” 來自 —— 資源。 https://mathworld.tw/Bifurcation.html
主題分類
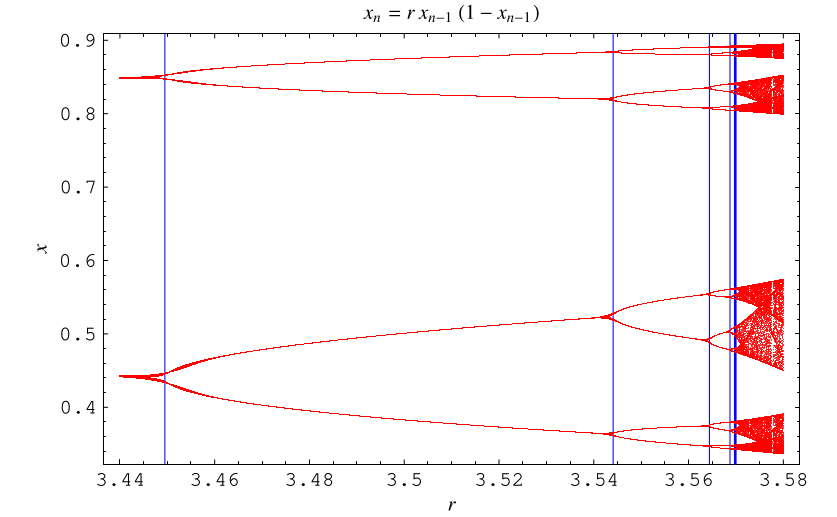
在變化。分岔有四種基本型別:翻轉分岔、摺疊分岔、叉形分岔和跨臨界分岔 (Rasband 1990)。

在變化。分岔有四種基本型別:翻轉分岔、摺疊分岔、叉形分岔和跨臨界分岔 (Rasband 1990)。