韋恩圖

一種在邏輯理論中使用的示意圖，用於描繪集合的集合並表示它們之間的關係。

上面說明了關於兩個和三個集合的韋恩圖。二階圖（左圖）由兩個相交的圓組成，總共產生四個區域，、、和 （空集，由沒有區域佔據表示）。這裡， 表示集合 和 的交集。

三階圖（右圖）由三個對稱放置的相互相交的圓組成，總共包含八個區域。標記為 、 和 的區域由僅在一個集合中且不在其他集合中的成員組成，標記為 、 和 的三個區域由在兩個集合中但不在第三個集合中的成員組成，區域 由同時在所有三個集合中的成員組成，而沒有區域佔據則表示 。

一般來說， 階韋恩圖是平面上 條簡單閉合曲線的集合，使得

1. 這些曲線將平面劃分為 個連通區域，並且

2. 的每個子集 對應於一個由 中曲線的內部的交集形成的唯一區域 (Ruskey)。

由於有 （二項式係數）種方法從總共 個成員中選取 個成員，因此 階韋恩圖中的區域數量為

（其中圖表外部的區域包含在計數中）。

在每個圓的中心位於其他兩個圓的交點的特殊情況下，三階韋恩圖中三個圓 的交集區域是被稱為勒洛三角形的幾何形狀。

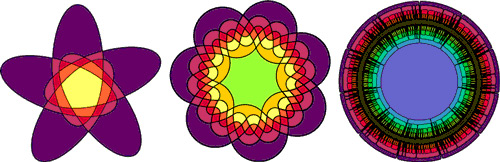
左上方左圖顯示了 Branko Grünbaum 的 韋恩圖，而中間圖中引人注目的 7 摺疊玫瑰花形是 Ruskey 稱為“維多利亞”的 韋恩圖。右圖顯示了 Ruskey、Carla Savage 和 Stan Wagon 最近構建的 上的對稱韋恩圖。

在電視罪案劇《數字追兇》(NUMB3RS) 第 4 季劇集“權力”中，數學天才查爾斯·埃普斯構建了一個韋恩圖，以確定符合特定描述且有暴力史的嫌疑人。