主題
Search

欠阻尼簡諧運動

DOWNLOAD Mathematica Notebook下載 Wolfram Notebook
SHOUnderdamped

欠阻尼簡諧運動是 阻尼簡諧運動 的一個特例

x^..+betax^.+omega_0^2x=0
(1)

其中

beta^2-4omega_0^2<0.
(2)

由於我們有

D=beta^2-4omega_0^2<0,
(3)

因此，數量

gamma=1/2sqrt(-D)
(4)
=1/2sqrt(4omega_0^2-beta^2)
(5)

是正數。將試探解 x=e^(rt) 代入微分方程，得到滿足以下條件的解

r_+/-=-1/2beta+/-igamma,
(6)

即，解的形式為 如下形式

x=e^(-(beta/2+/-igamma)t).
(7)

使用 尤拉公式

e^(ix)=cosx+isinx,
(8)

這可以被重寫為

x=e^(-(beta/2)t)[cos(gammat)+/-isin(gammat)].
(9)

我們對實數解感興趣。由於我們在這裡處理的是線性齊次常微分方程，線性無關 解的線性組合也是解。由於我們在 (9) 中有這樣的解的和，因此 虛部 和 實部 分別滿足常微分方程，因此是我們要求的解。正弦項前面的常數是任意的，所以我們可以將解識別為

x_1=e^(-(beta/2)t)cos(gammat)
(10)
x_2=e^(-(beta/2)t)sin(gammat),
(11)

所以通解是

x=e^(-(beta/2)t)[Acos(gammat)+Bsin(gammat)].
(12)

初始值為

x(0)=A
(13)
x^.(0)=-1/2betaA+B,gamma
(14)

所以 A 和 B 可以用初始條件表示為

A=x(0)
(15)
B=(betax(0))/(2gamma)+(x^.(0))/gamma.
(16)

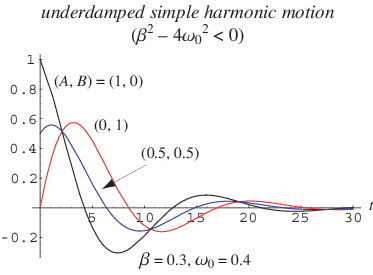
上面的圖顯示了一個欠阻尼簡諧振盪器，引數為 omega=0.3 和 beta=0.4，針對各種初始條件 (A,B)。

對於一個具有餘弦強制函式的欠阻尼振盪器 g(t)=Ccos(omegat)，因此

x^..+betax^.+omega_0^2x=Ccos(omegat),
(17)

定義

gamma=1/2sqrt(4omega_0^2-beta^2)
(18)
alpha=1/2beta
(19)

為了方便起見，然後注意

4omega_0^2-beta^2=4gamma^2
(20)
omega_0^2=gamma^2+1/4beta^2
(21)
=gamma^2+alpha^2
(22)
beta=2alpha.
(23)

我們現在可以使用引數變分法來獲得特解，如下所示

x^*=x_1v_1+x_2v_2,
(24)

其中

v_1=-int(x_1(t)g(t))/(W(t))
(25)
v_2=int(x_2(t)g(t))/(W(t))
(26)

朗斯基行列式為 朗斯基行列式

W(t)=x_1x^._2-x^._1x_2
(27)
=gammae^(-2alphat).
(28)

這些可以直接積分得到

v_1=-C/gammainte^(alphat)sin(gammat)cos(omegat)dt
(29)
v_2=C/gammainte^(alphat)cos(gammat)cos(omegat)dt.
(30)

因此，

x^*(t)=C((alpha^2+gamma^2-omega^2)cos(omegat)+2alphaomegasin(omegat))/([alpha^2+(gamma-omega)^2][alpha^2+(gamma+omega)^2])
(31)
=C/(sqrt((omega_0^2-omega^2)^2+omega^2beta^2))cos(omegat+delta),
(32)

其中使用了 和角公式 以及

delta=tan^(-1)((betaomega)/(omega^2-omega_0^2)).
(33)

另請參閱

臨界阻尼簡諧運動, 阻尼簡諧運動, 過阻尼簡諧運動, 簡諧運動

使用 探索

參考文獻

Papoulis, A. Probability, Random Variables, and Stochastic Processes, 2nd ed. 紐約：McGraw-Hill，第 525-527 頁，1984 年。

請引用本文為

Weisstein, Eric W. "欠阻尼簡諧運動。" 來自 Web 資源。 https://mathworld.tw/UnderdampedSimpleHarmonicMotion.html

主題分類