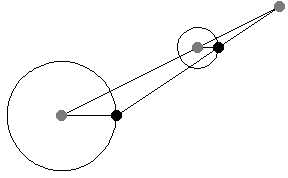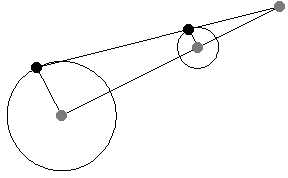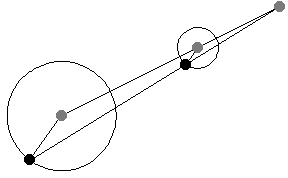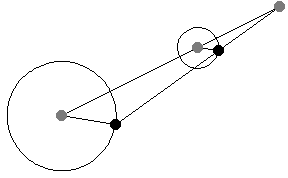
連線位似圖形的對應點的直線的交點。在上圖中, 是位似圖形
和
的位似中心。對於相似但不具有平行邊的圖形,存在相似中心(Johnson 1929,第 16-20 頁)。
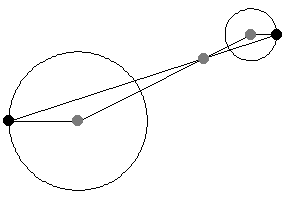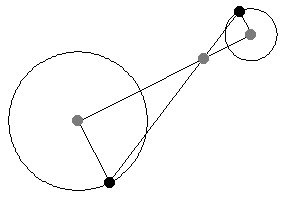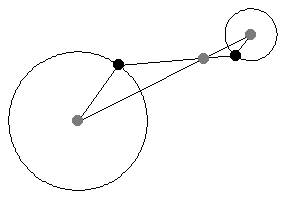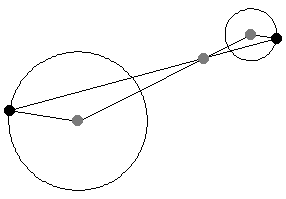
給定兩個非同心圓,繪製半徑,使其平行且方向相同。然後,連線半徑端點的直線穿過中心連線上的一定點,該點將中心連線按半徑之比外分。此點稱為外位似中心,或外相似中心(Johnson 1929,第 19-20 和 41 頁)。
如果半徑被繪製為平行,但方向相反,則半徑的端點穿過中心連線上的一定點,該點將中心連線按半徑之比內分(Johnson 1929,第 19-20 和 41 頁)。此點稱為內位似中心,或內相似中心(Johnson 1929,第 19-20 和 41 頁)。
對於半徑為 、中心為
以及線段角度為
的兩個圓,位似中心的位置透過解以下聯立方程組給出
|
(1)
| |||
|
(2)
|
求解 ,其中
|
(3)
| |||
|
(4)
|
加號給出外位似中心,而減號給出內位似中心。
|
|
如上圖所示,當平行線段的角度變化時,位似中心的位置保持不變。這一事實為將一個半徑的圓周運動轉換為另一個半徑的圓周運動提供了一種(開槽)連桿機構。
三個圓的六個位似中心,每三個共線,共四條線(Johnson 1929,第 120 頁),這些線“包圍”著最小的圓。