邊長為 的直角 等腰三角形膜的運動方程,其邊沿正
軸和
軸方向,由下式給出
其中
且 ,
為 整數,其中
。此解可以透過從一個正方形膜的兩個波動解中減去索引反轉的解得到。由於對角線上與中心等距的點必須具有相同的波動方程解(透過對稱性),因此只要
和
都是偶數或奇數,此過程給出的波函式將沿對角線消失。我們必須進一步限制模式,因為那些
的模式給出的波函式只是 負
,而
給出的波函式完全為零。
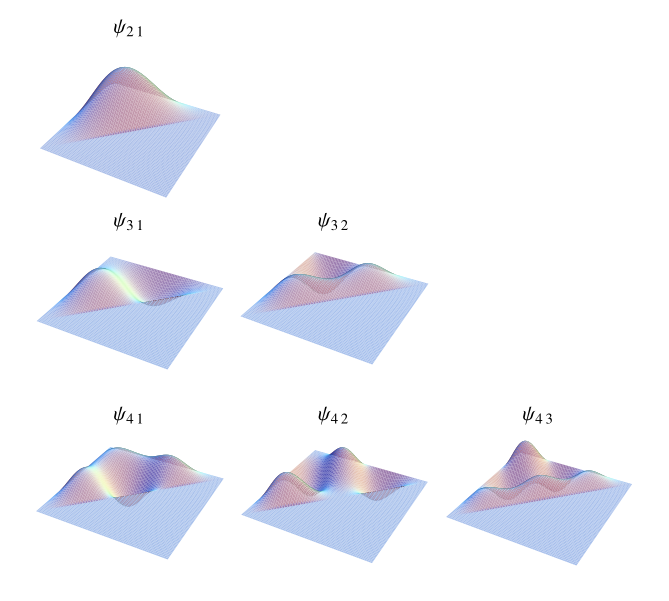
上面的圖顯示了最低階的空間模式。

邊長為 的直角 等腰三角形膜的運動方程,其邊沿正
軸和
軸方向,由下式給出
其中
且 ,
為 整數,其中
。此解可以透過從一個正方形膜的兩個波動解中減去索引反轉的解得到。由於對角線上與中心等距的點必須具有相同的波動方程解(透過對稱性),因此只要
和
都是偶數或奇數,此過程給出的波函式將沿對角線消失。我們必須進一步限制模式,因為那些
的模式給出的波函式只是 負
,而
給出的波函式完全為零。
上面的圖顯示了最低階的空間模式。
Weisstein, Eric W. "波動方程——三角形。" 來自 —— 資源。 https://mathworld.tw/WaveEquationTriangle.html