三角正雙 Cupola

三角正雙 Cupola 是 約翰遜多面體 ，由八個等邊三角形和六個正方形組成。如果三角正雙 Cupola 上下以三角形為底面放置，則可以將上下兩部分互相旋轉六分之一圈，得到截角立方八面體。

三角正雙 Cupola 的體積為

(1)

以及 Dehn 不變數為

			(2)
			(3)

其中第一個表示式使用了 Conway et al. (1999) 的基。它可以被分解為截角立方八面體，它與截角立方八面體的區別僅在於頂部和底部 cupola 的相對旋轉。

在六方最密堆積中，球體層以交替層中的球體彼此重疊的方式堆積。與立方最密堆積一樣，每個球體被 12 個其他球體包圍。取 13 個這樣的球體的集合得到如上所示的簇。連線外部 12 個球體的中心得到 (Steinhaus 1999, pp. 203-205)。

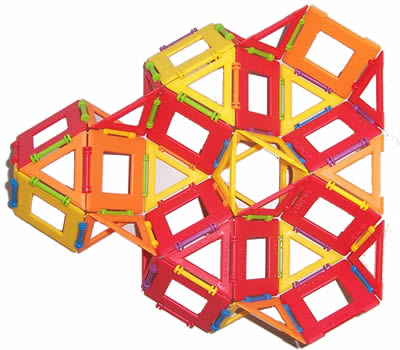
雖然它不是空間填充多面體，但當與八面體組合時，它可以填充空間，如上圖所示（照片由 Ed Pegg, Jr. 提供，私人通訊，2004 年 9 月 23 日）。