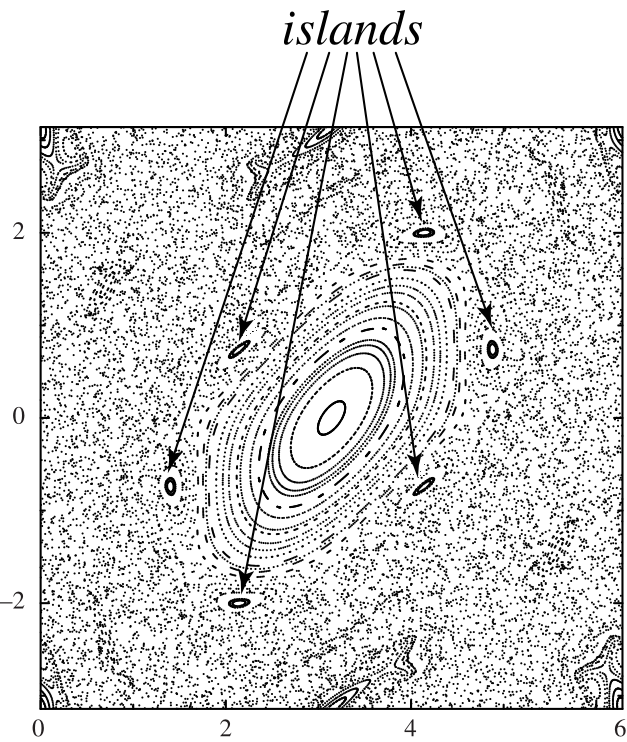
如果一個可積的準週期系統受到輕微擾動,以致其變為不可積的,那麼由於模式鎖定,只有有限數量的 -對映迴圈會保留下來。其中一個將是橢圓形的,另一個將是雙曲線形的。
圍繞橢圓不動點的是一個穩定的對映軌道區域,它們圍繞該不動點旋轉,如上面的標準對映所示,其中。當迭代地應用對映時,島被對映到圍繞橢圓迴圈的下一個點的類似結構。因此,對映具有一個島鏈,其不動點在橢圓(位於島的中心)和雙曲線(在島之間)之間交替。由於未擾動的系統會經歷無窮個有理值,因此擾動的系統必須具有無窮多個島鏈。

如果一個可積的準週期系統受到輕微擾動,以致其變為不可積的,那麼由於模式鎖定,只有有限數量的 -對映迴圈會保留下來。其中一個將是橢圓形的,另一個將是雙曲線形的。
圍繞橢圓不動點的是一個穩定的對映軌道區域,它們圍繞該不動點旋轉,如上面的標準對映所示,其中。當迭代地應用對映時,島被對映到圍繞橢圓迴圈的下一個點的類似結構。因此,對映具有一個島鏈,其不動點在橢圓(位於島的中心)和雙曲線(在島之間)之間交替。由於未擾動的系統會經歷無窮個有理值,因此擾動的系統必須具有無窮多個島鏈。
Weisstein, Eric W. "島." 來自 -- Wolfram 網路資源. https://mathworld.tw/Island.html