圖橋

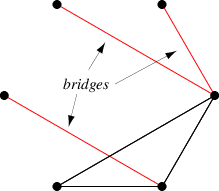
連通圖的橋是一條圖邊，移除該邊會使圖斷開連線（Chartrand 1985, p. 45; Skiena 1990, p. 177）。更廣義地，橋是一個不一定連通的圖 的一條邊，移除該邊會增加 的連通分量數（Harary 1994, p. 26; West 2000, p. 23）。

連通圖的一條邊是橋當且僅當它不位於任何環上。因此，橋不可能是環弦。

橋也稱為割邊（West 2000, p. 23）或割弧。

樹的每條邊都是橋。連通三次圖包含橋當且僅當它包含割點（Skiena 1990, p. 177），即，如果它不是雙連通圖。

包含一個或多個橋的圖被稱為有橋圖，而沒有橋的圖稱為無橋圖。

Wolfram 語言 函式FindEdgeCut[g] 返回圖的最小尺寸的邊割集，如果集合大小為 1，則對應於圖橋。可以使用以下命令列出許多命名圖的預計算橋：GraphData[graph,"Bridges"].

頂點的圖橋的類似物稱為割點。