主題
Search

第二類完全橢圓積分

DOWNLOAD Mathematica Notebook下載 Wolfram Notebook
EllipticE
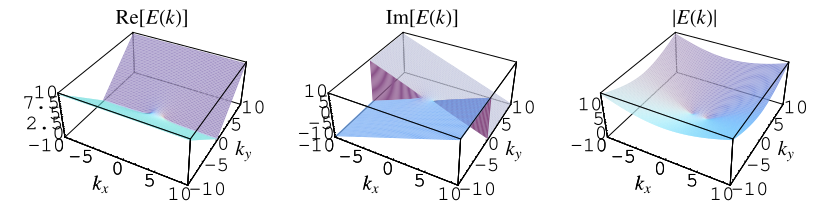
EllipticEReIm
EllipticEContours

第二類完全橢圓積分，如上圖所示為 k 的函式，定義為

E(k)=E(1/2pi,k)
(1)
=pi/2{1-sum_(n=1)^(infty)[((2n-1)!!)/((2n)!!)]^2(k^(2n))/(2n-1)}
(2)
=1/2pi_2F_1(-1/2,1/2;1;k^2)
(3)
=int_0^(K(k))dn^2(u,k)du,
(4)

其中 E(phi,k) 是第二類不完全橢圓積分，_2F_1(a,b;c;x) 是超幾何函式，而 dn(u,k) 是 Jacobi 橢圓函式。

它在 Wolfram Language 中實現為EllipticE[m]，其中 m=k^2 是引數。

對於 k=k_n 的特殊值，E(k) 可以用 K(k_n) 和橢圓 alpha 函式 alpha(n) 以閉合形式計算，其中 k_n 稱為橢圓積分奇異值。其他特殊值包括

E(0)=1/2pi
(5)
E(1)=1.
(6)

第二類完全橢圓積分滿足勒讓德關係式

E(k)K^'(k)+E^'(k)K(k)-K(k)K^'(k)=1/2pi,
(7)

其中 K(k) 和 E(k) 分別是第一類和第二類完全橢圓積分，而 K^'(k) 和 E^'(k) 是互補積分。其導數為

(dE)/(dk)=(E(k)-K(k))/k
(8)

(Whittaker and Watson 1990, 第 521 頁)。

EllipticEODE

微分方程的解為

k^('2)d/(dk)(k(dy)/(dk))+ky=0
(9)

(Zwillinger 1997, 第 122 頁；Gradshteyn and Ryzhik 2000, 第 907 頁) 由下式給出

y=C_1E(k)+C_2[E^'(k)-K^'(k)].
(10)

如果 k_r 是一個奇異值（即，

k_r=lambda^*(r),
(11)

其中 lambda^* 是橢圓 lambda 函式），並且 K(k_r) 和橢圓 alpha 函式 alpha(r) 也已知，則

E(k)=(K(k))/(sqrt(r))[pi/(3[K(k)]^2)-alpha(r)]+K(k).
(12)

另請參閱

第一類完全橢圓積分, 第三類完全橢圓積分, 橢圓 Alpha 函式, 第二類橢圓積分, 橢圓積分奇異值

相關的 Wolfram 網站

http://functions.wolfram.com/EllipticIntegrals/EllipticE/

使用 探索

參考文獻

Gradshteyn, I. S. and Ryzhik, I. M. 積分表、級數與乘積表，第 6 版 San Diego, CA: Academic Press, 2000.Whittaker, E. T. and Watson, G. N. 現代分析教程，第 4 版 Cambridge, England: Cambridge University Press, 1990.Zwillinger, D. 微分方程手冊，第 3 版 Boston, MA: Academic Press, p. 122, 1997.

在 中被引用

第二類完全橢圓積分

請引用為

Weisstein, Eric W. “第二類完全橢圓積分。” 來自 Web 資源。 https://mathworld.tw/CompleteEllipticIntegraloftheSecondKind.html

學科分類