蚌線三等分角線是一種 三等分角線，是 玫瑰線 的一個特例，其 
（可能經過平移、旋轉和縮放）。 阿基米德以及 Étienne Pascal 在 1630 年研究了它。
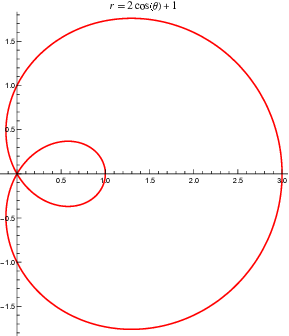
在其最常見的標準形式中，蚌線三等分角線具有 極座標方程
 |
(1)
|
（Ferréol）。 它可以表示為 笛卡爾方程
 |
(2)
|
或
 |
(3)
|
蚌線三等分角線是相對於其蚌線圓中心而言的 心臟線踏板曲線（Ferréol）。
它具有 弧長
 |
(4)
|
其中 
是 第二類完全橢圓積分。 它的外邊界包圍的面積為
 |
(5)
|
其內部環的面積為
 |
(6)
|
的一個特例， |
(7)
|
這必須旋轉 
度，按 2 的因子縮放，向右平移距離 1，並從 
到 
繪製，以獲得標準形式的曲線。
