n-流形 和
的連通和
是透過刪除
-球
在
的內部,並將由此產生的穿孔流形
透過同胚
相互連線而形成的,因此
需要 在
的內部,且
在
中是雙領的,以確保連通和是一個流形。
在拓撲上,如果 和
是道路連通的,那麼連通和與
和
上連線被粘合的位置的選擇無關。
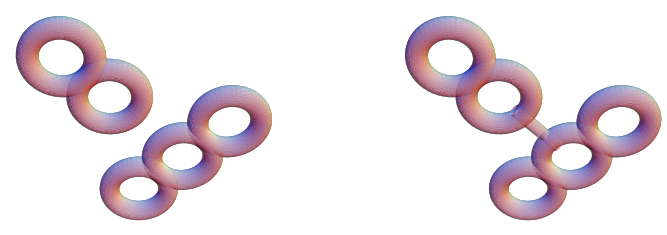
上面的圖示顯示了兩個環面(頂部圖)和兩對多把環面的連通和。
n-流形 和
的連通和
是透過刪除
-球
在
的內部,並將由此產生的穿孔流形
透過同胚
相互連線而形成的,因此
需要 在
的內部,且
在
中是雙領的,以確保連通和是一個流形。
在拓撲上,如果 和
是道路連通的,那麼連通和與
和
上連線被粘合的位置的選擇無關。
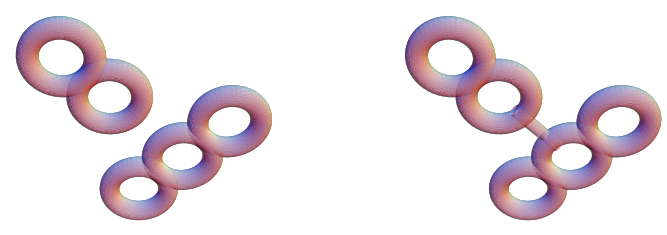
上面的圖示顯示了兩個環面(頂部圖)和兩對多把環面的連通和。
本條目的部分內容由 Todd Rowland 貢獻
Rowland, Todd 和 Weisstein, Eric W. "連通和。" 來自 --一個 資源。 https://mathworld.tw/ConnectedSum.html